|
|
 |
|
Wulffman is a program for interactively examining the Wulff shapes of crystals with specified symmetries. The Wulff shape is the shape that possesses the lowest surface energy for a fixed volume, and hence represents the ideal shape that the crystal would take in the absence of other constraints. For a periodic crystal, i.e., one that can be generated by periodic repetition of a simple unit cell , the Wulff shape must be consistent with the crystallographic point group symmetry of the underlying crystal. The point group is simply the set of all point isometries (rotations, roto-inversions, and reflections) that leave the environment around a point unchanged. In the most general case, the Wulff shape will be a convex polyhedron whose faces (facets) correspond to crystal planes that are low in energy. In some cases, Wulff shapes appear in more complex circumstances. For example, a precipitate at an interphase grain boundary in a material will in many cases have a shape that corresponds to a combination of the Wulff shapes for the pure materials on either side of the boundary. The Wulff shape in these cases is the intersection of two Wulff shapes that may or may not have displaced origins and rotated reference frames (coordinate systems). Wulffman possesses the capability to construct intersections of an arbitrary number of Wulff shapes, each of which can have a different symmetry, origin, and orientation of coordinates. Wulffman requires the point group symmetry of a crystal (or crystals) of interest, a set of crystal planes (facets) for each symmetry, and their respective surface energies. From this information, Wulffman constructs the Wulff shape and sends its output to Geomview , a 3-D visualization tool. Surface energies can be changed at will, and Wulffman reconstructs the lowest energy polyhedron. In this manner, the user can directly and easily visualize the effects of surface energy anisotropy on the equilibrium forms of crystals. A simple example of Wulff shape construction and intersection is
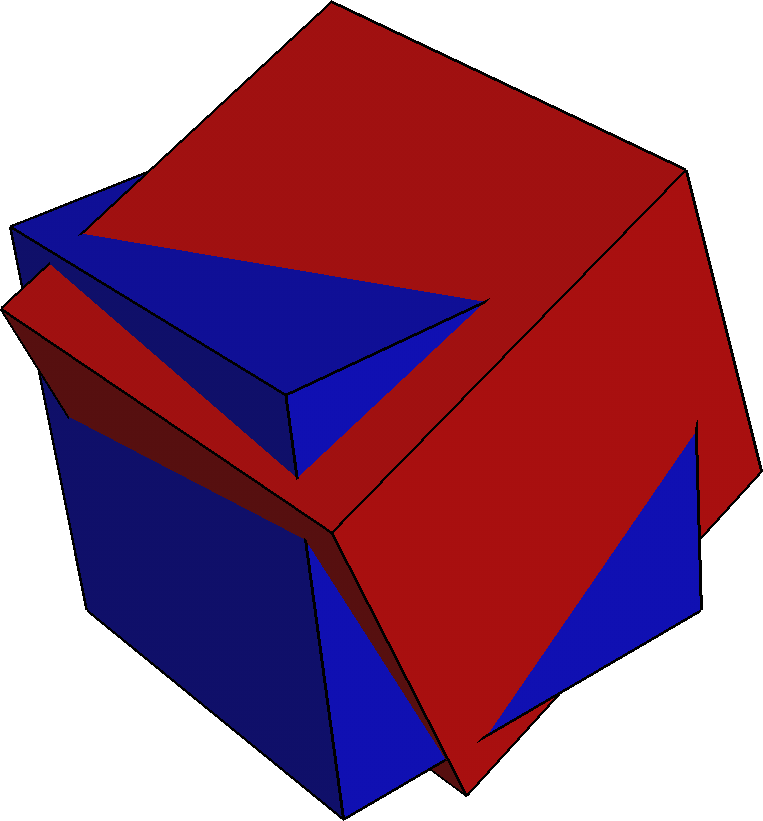
illustrated in Figure 1. Cubic symmetry is chosen for two Wulff shapes
with slightly displaced origins. The [100] facet direction is
selected for each Wulff shape, and the coordinate system of shape 2 is
rotated around the 113 axis of shape 1 by 33 degrees.
The individual Wulff shapes are, of course, cubes (Figures 1a and 1b)
that are rotated with respect to one another. If we simply overlap
these cubes, the resulting shape is the (non-convex) polyhedron in
Figure 1c. This does not, however, correspond to the intersected
Wulff shape, since a convex polyhedron with lower surface energy can
be constructed. The final intersected Wulff shape is the convex shape
shown in Figure 1d.
Center for Theoretical and Computational Materials Science, NIST Questions or comments: wulffman@ctcms.nist.gov |



 Overview
Overview