|
|

 WulffmanDocumentation
WulffmanDocumentation

| Table Of Contents
| 
|
Wulffman is a module to be used with Geomview, a 3-D
visualization environment written by the Geometry Center at the
University of Minnesota. The best way to learn how to use Wulffman is
to experiment; it won't bite! The basic procedure for running
WUlffman is as follows:
- Start Geomview
- Within the Modules panel of the Geomview window, click
on Wulffman . The Wulffman
control window should become visible.
- Open the Symmetry Tool and select a point group.
- Open the Facet Tool and enter some facets of interest
- Click Go in either the Control or Facet
Windows. The Wulff shape should be generated and output to
Geomview.
For a description of the details of Wulffman, read
the documentation below, or use the on-line Help
contained in each Wulffman window. The HTML documents and those
contained within the program contain the same content, although there
are no graphics within the program Help.
Wulffman is designed to construct the global Wulff shape that
results from the intersection of one or more constituent Wulff shapes.
The Global Shape Window in Wulffman is
used to spawn, close, or destroy all of the windows associated with
each sub-shape. Each individual sub-shape has its own
set of specifications (Symmetry, Facets, Preferences,...) each of
which is controlled by a distinct set of windows. The actual Wulff
shape displayed by Geomview can then be either one of the
individual sub-shapes or the intersection of any subset of all
possible sub-shapes. A schematic representation of the relationship
between the global window and all of the individual windows is shown
below.
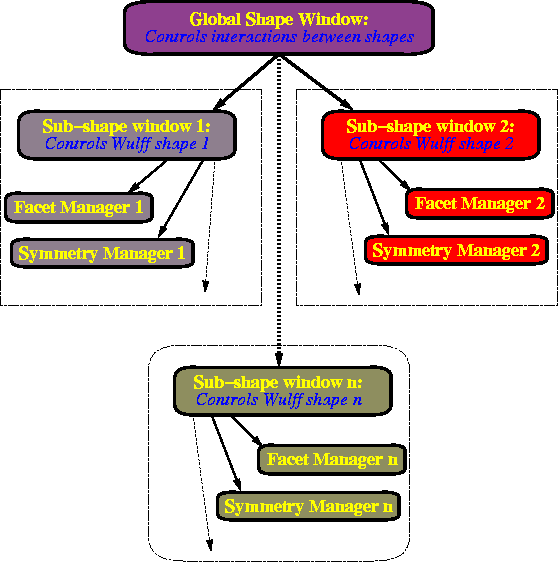
Window interrelationships in Wulffman. The Global Shape
Window (top) control the existence of all sub-shape windows (Labeled
windows 1, 2, and n for convenience).
The basic layout of the program invovles separation of the primary
functions of the code into "Tool" windows and "Information" windows.
Tool windows contain tools that the user can use to manipulate the
program. Information windows contain information about selected
aspects of each of the tools. Each primary window contains a colored
field in the upper left portion of the window indicating its name.
- Normal
- These buttons perform a simple function when pressed and do not
remain active after their selection. An example of a
normal button is the Close button present in all windows.
- Toggle
- These buttons control Wulffman's tool and information windows.
When a toggle is activated, it changes color and the desired window
is opened; closing the window acts to release the toggle,
as does pushing the toggle while the window is active. Most
of the buttons in the Main Window are toggles.
- Exclusive
- "Exclusive" buttons are used to select between a group of
mutually exclusive options. When an exclusive button is active, it is
colored, and selection of other buttons within its group automatically
deactivates it. An example of this can be found in the selection of
crystal systems .
There are two buttons that are used throughout the application:
the Close and Help buttons. Close acts to close the
window in which it is pressed, usually activating a toggle
in the Main Window . The Help button
brings up help about the features of the window in which it is
pressed; global help is available by pressing Help in the
Main window.
There are several instances where the user is presented with data
fields that can be edited. Instances of editable data fields occur in
the Facet Tool, Custom Tool, Matrix Info, and Coord Xform windows. An
editable data field appears as a "down" box, and clicking on it with
the mouse generates a cursor. Normal keystrokes and cursor movement
commands then function within this field. Some data fields are
not always editable by the user. These fields are represented by
simple flat boxes around the data in question (see Coord Xform for an example). Clicking on
these fields will have no effect .
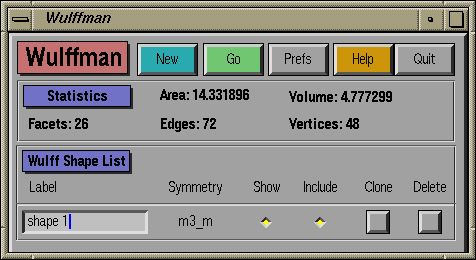
This window controls all the Wulff shapes at once. It allows you to
create new shapes, duplicate existing ones, and delete shapes. It also
controls the intersection of shapes and provides statistics about
the shape being shown by Geomview. The five buttons at the top of the
window function as follows:
- New: Add a new shape to the list
and open up its Main window.
- Go: Build the Wulff shape.
- Prefs: Opens and closes the Preferences control window.
- Help: Opens and closes a global help window.
- Quit: Exit Wulffman. This will NOT delete the shape
shown by Geomview.
Information can be found in the Statistics section about the
displayed shape including the surface area, contained volume, and the
total numbers of facets, edges, and vertices displayed by Geomview. Note
that Euler's theorem governs the relationship between these three
quantities: v - e + f = 2.
At the bottom of the window is a list of all the shapes which will be
intersected to form the final shape. For most applications, only one
Wulff shape will be examined. Each shape is described with one line on the
form. From left to right:
- A Label that will identify windows
associated with this shape.
- The current Symmetry group of the shape.
- A toggle button that controls whether windows associated with
this shape are Shown or not.
- A toggle button indicating whether to Include this shape in
the final intersection or not.
- The Clone button produces another shape having the same
symmetry and normals as the current shape. This is useful if
you wish to intersect two identical shapes with different
offsets or orientations.
- The Delete
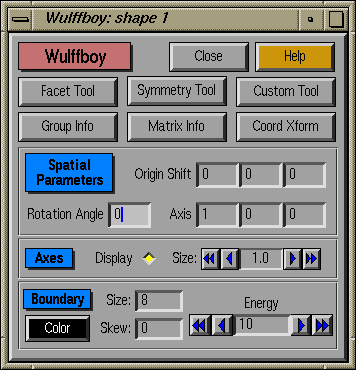
This is the primary control window for an individual shape. It allows
access to other
Tool and Information windows, and gives additional status about the
current state of the program. The six control buttons (specified
below) are all toggles
that open their respective windows. Help brings up help
about this window. Close closes this window and all
subsidiary windows, and pops up the show button on the Meta form.
Tools for Building Wulff Shapes:
Information Tools:
- Group Info :
Obtain information about the selected symmetry group
- Matrix Info :
Browse symmetry matrices
- Coord Xform :
Transformation between Cartesian and Unit Cell coordinates
Spatial parameters:
- Origin Shift: The center of this Wulff shape is offset by
a vector according to these three input fields. If you shift
the origin of any Wulff shapes very far, you should be careful
to enter a center point in the Preferences
Form.
- Rotation Angle: Rotate the Wulff shape by this angle (in
degrees) around the Rotation Axis.
- Rotation Axis: The vector about which the Wulff shape
will be rotated. Note that only the direction is important: the
magnitude will have no effect.
Axes:
- Show : Toggle that determines whether
coordinate axes (either cell or Cartesian) are shown along with the
Wulff shape.
- Size : Allows adjustment of the size of
the axes. Double and single arrows allow large or small incremental
modifications of their length.
This section controls the features of the Boundary
Polytope . This is a polytope that surrounds the
Wulff shape at any given time; by default it is invisible, but note
that each shape can have its own Boundary Polytope. The shape
of this polytope is
controlled by the Size and Skew parameters, and its
volume is controlled by the Energy. The number of facets on the
polytope is given by Size.
The orientation of facets is determined by Skew
. For Skew = 0, the facets are uniformly distributed
over the surface of a sphere. For large values of
Skew , the facets are distributed over the surface of a sphere
with the additional constraint that they are repelled from
orientations that correspond to user-defined facets. The strength of
the repulsion is proportional to the value of Skew.
- Color : The default color appears as
black, but is actually transparent (the first entry in the colormap).
- Size: Number of facets in the bounding polyhedron
- Skew: Degree to which facets on the bounding
polytope are skewed away from user-defined facets. A large value of
the skew effectively creates more facets on the bounding polytope,
assuming that this polytope intersects the Wulff shape.
- Energy: Surface energy of the bounding polytope.
A large value of the surface energy (i.e., much larger than that of
the user-defined facets) will generate a bounding polytope that lies
completely outside the Wulff shape. For energy values less
than or equal to the energies of facets defined by the user, the
bounding polytope effectively acts as an isotropic surface between
facets (for a large enough value of Size ).
The Facet Tool controls the facets that will be present in the Wulff
shape. Each facet is specified by its normal, i.e., the unit vector
perpendicular to that plane. A surface energy for each facet can then
be specified (the default is for isotropic surface energy). Once all
of the information is entered by the user in this window, it must be
exported to Wulffman for shape construction.
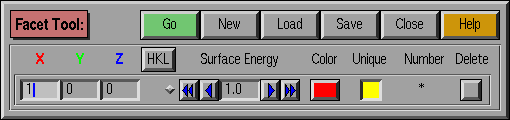
- Go : Generate / Update the Wulff shape
- New : Create a new (unspecified) facet
- Load :
Read in a set of stored facets. This
buttong spawns a window allowing the user to locate the file
containing the facets of interest. Within this load window, if the
Overwrite button is lit, the facets that are read in will
replace any existing list of facets. If it is not lit, then the
facets that are read in are simply appended to the existing list. The
symmetry group and crystal class associated with the loaded
facets are set automatically. However, in the case of a set of
facets corresponding to a Custom group, the custom group is not
loaded; the custom group window is displayed and the user can
load the appropriate custom group at that time.
- Save :
Save a group of facets (including the crystal
class and the point group).
No information about the boundary polyhedron is saved, and the current
group name is only saved for reference purposes.
- XYZ / HKL : (XYZ / HKL / UVW in V1.2.3)
Facet specifications in either
Cartesian or unit cell coordinates (or Miller indices in V1.2.3).
Each "down" box is an editable
field which holds facet normal directions. The current coordinate
system is indicated by the colored letter above these fields.
XYZ indicates cartesian coordinates, HKL indicates unit cell
coordinates (Miller indices in V1.2.3+, with UVW indicating unit
cell coordinates).
- XYZ / HKL Selection Button: (XYZ / HKL / UVW in V1.2.3
Choose between facet
specification in Cartesian (XYZ) or Unit Cell (HKL) coordinates.
Pushing this button shifts the facets to the coordinate system
indicated, i.e., if the button reads HKL, then pushing it indicates
facets should be input in HKL coordinates. In version 1.2.3, HKL indicates
Miller indices, and UVW is used to indicate cell coordinates: the button
is a triple-toggle, cycling between the three choices.
- "On-the-Fly" Toggle:
Update the Wulff shape automatically
as surface energy is changed (small light button located to the left
of the surface energy controls).
- Surface energy :
The value of the surface energy
for each facet is controlled in this editable data field. Arrow
buttons allow the value to be changed by large (>>) or small (>)
preset increments. Clicking each button changes the surface energy by
a given increment; holding down the button changes the surface energy
continuously until released. Alternatively, the actual value of the surface
energy can be changed directly in its field.
- Unique :
Toggle button that allows the user to specify whether the symmetry
group operations will act on the given facet (default = TRUE). If
this button is selected (yellow), then the facet is unique (i.e., it
is a single crystallographic plane).
- Number :
The total number of symmetry-distinct facets of this type generated by
the action of the symmetry group. Note that this is not
necessarily the number of facets that are visible in Geomview on the
Wulff shape.
- Color :
Choose the color for the given facet.
Note that the first color of the colormap (black) is actually
transparent, so that facets can be made to effectively disappear.
Note in addition that entries can be added to the colormap through the
Preferences control window.
- Delete : Delete the given facet from the working set
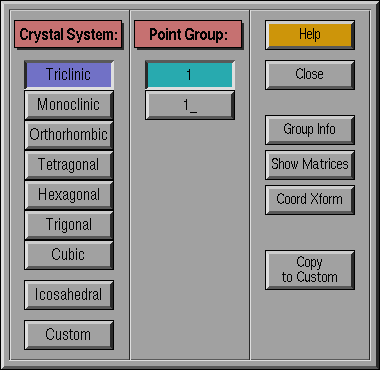
Select the crystal system for use. These buttons all represent
mutually exclusive options, hence only one system may be selected at
any given time. Systems are divided into three categories: (1)
crystallographic systems (those that are consistent with translational
periodicity), (2) Icosahedral systems (those that possess the symmetry
of one of the icosahedral point groups), and (3) Custom systems.
Icosahedral systems are not consistent with tranlsational periodicity;
custom systems, i.e., those defined by the user, are consistent with
translational periodicity only if the custom group defines a subgroup of
one of the crystallographic groups. In general, a custom system will
not be consistent with translation, and hence is characterized below
as non-crystallographic.
- Crystallographic systems: Select the crystal system /
Bravais lattice for use
- Triclinic
- Monoclinic (c-axis unique)
- Orthorhombic
- Tetragonal
- Trigonal (Hexagonal axes)
- Hexagonal
- Cubic
- Non-crystallographic systems:
- Icosahedral : Choose groups possessing
icosahedral symmetry
- Custom : Select a custom group
Output in the point group field depends on what crystal system has
been selected. If one of the crystallographic systems has been
selected, then buttons for the crystallographic point groups
corresponding to that crystal system will be revealed. If the
icosahedral system is chosen, then buttons for the two icosahedral
point groups will be displayed. If Custom is selected, buttons for
custom groups will be displayed. If the user has not defined any
custom groups, then these buttons will just display Custom 1
through Custom 6 . The user then needs to Edit the
custom groups; this will have the effect of changing one of the
displayed Custom buttons to reflect the set of symmetry elements
specified.
Additional Actions:
- Group Info : Get
information about the selected crystallographic groups
- Show Matrices : Show
the 3x3 matrices corresponding to the generators for the given group.
- Coord Xform : View or
edit unit cell parameters for the chosen crystal system that affect
the global XYZ/HKL transformation.
- Copy to Custom : (Visible only when
non-custom group selected)
Copy the selected crystallographic group to a custom
group. This feature is useful if one wishes to add non-crystallographic
symmetry elements to a crystallographic group.
- Custom group actions: (Visible only when [Custom] selected)
- Load : Load a custom group
- Edit : Edit one of the defined custom
groups or create a new custom group if none are defined.
- Save : Save the currently selected custom
group to file.
The Custom Tool allows the user to define a custom symmetry group.
The user can choose rotations, roto-inversions, and mirror reflections to
define the symmetry elements in the group. Each rotation axis is
defined as a rotation by 360/n degrees, where the user supplies
n and the direction around which the rotation occurs. Mirror
planes are defined by their normals. Roto-inversion axes are defined by
selecting the roto-inversion toggle in the rotations field. Global
inversion symmetry is selected using the Inversion toggle.
Users can also input symmetry manually in the form of their 3x3
matrices.
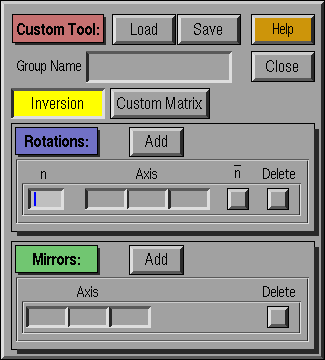
- Group Name : Select a name for the current custom group
- Load : Load the elements from a previously defined
group.
- Save : Save the current symmetry elements to a
custom group.
- Inversion : Toggle for global inversion symmetry
- Custom Matrix : Input a symmetry matrix manually
- Rotations:
- Add: Add a new axis to the working set
- n: Order of rotation (360/n degrees)
- Axis: Select the axis about which the rotation occurs.
- n_: Roto-inversion toggle (Default = No
roto-inversion, Yellow = Roto-inversion Axis)
- Delete : Delete this axis from the working set.
- Mirrors:
- Add : Add a new mirror plane
- Axis : Normal direction of mirror plane
- Delete : Delete this mirror plane from the
working set.
This window allows modification of some of the more detailed
control features associated with construction of the Wulff shape.
Any changes made to input parameters do not take effect immediately.
The user must press a carriage return in any of the editable fields
for these changes to take effect.
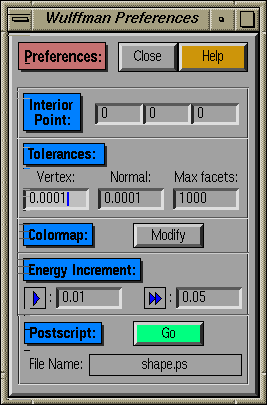
- Interior Point:
In order to use the fast Qhull algorithm to compute the
Wulff shape, we need to know a priori one point that
will be interior to the end shape. With just a single Wulff
shape, this is trivially the center of the Wulff shape, but if
two or more shapes are intersected, finding such an interior
point can be non-trivial. Thus, we leave it up to the user.
- Tolerances:
- Vertex:
The minimum distance between vertices that are to be
considered distinct. Any vertices generated by action
of symmetry operations that are separated by distances
smaller than this value will be considered the same vertex.
- Normal:
The minimum distance between normals defining distinct
facets (similar in spirit to Vertex tolerance).
- Max Facets:
The maximum number of facets allowed in any given Wulff
shape. The primary function of this value is to
control situations where an unreasonably large number of
facets are generated by action of the symmetry group.
An example of such a situation would be if a user
defined a rotation group that involved rotations by some
infinitesmal angle. Under the action of such a group, a
huge number of equivalent facets could be generated. These
situations should, in general, be avoided.
- Colormap:
This button allows modification of the existing colormap. It
allows for modification of existing colors or addition of new colors.
A new color is added by simply clicking on one of the black fields
below existing colormap entries. A pop-up window then allows the user
to either choose from a group of predefined colors or specify the RGB
values for a custom color. Note that existing colormap entries can be
modified, but this is likely to have unwanted side-effects on the
appearance of the windows within Wulffman.
- Energy Increment:
These input fields allow the user to adjust how rapidly the
surface energy will change when the energy arrows are clicked
in the Facet Tool. The large and
small increments can be changed independently.
- Postscript:
Also known as "a Wulff in sheets, folding".
This feature allows you to print out a version of your Wulff
shape. Select a file name and hit this Go button, and a
flattened version will be produced as PostScript scaled to fit
on one 8.5"x11" piece of paper (with a small border for color
printers). With some cutting, folding, and taping, you can
produce a real model of your Wulff shape.
This window displays selected information about the current
crystallographic group. For each group, there is a finite set of
symmetry operations, the number being the order n of the group. The
action of each symmetry element on a point in three-dimensional space
creates an equivalent point , i.e., one that is equivalent to
the first under the given symmetry operations. If one were to operate
the entire group on this point, a set of m equivalent points
would be generated, where m is less than or equal to n, the group
order.
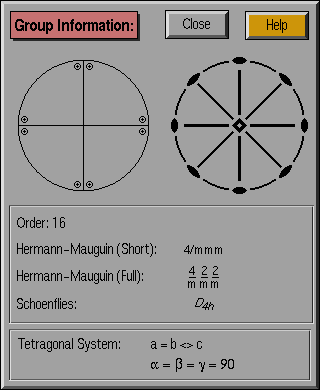
- Equivalent points:
The graphic in the upper left of the
window is the stereographic projection of the set of points equivalent to
a general point. A representative stereographic projection is given
in Figure 1.
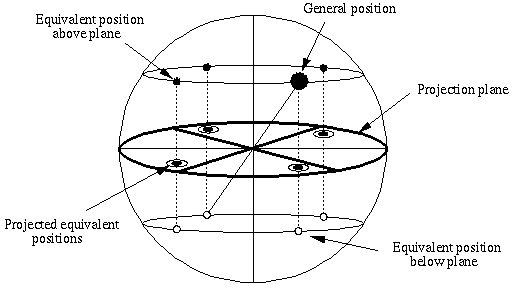
Figure 1:: Locate a
general position (large filled circle) on the
surface of a sphere centered at the origin. The action of each symmetry
element of the point group on the vector to the general position
generates an equivalent position. Equivalent positions can either be
above (small filled circles) or below (open circles) the equatorial
plane of the sphere (denoted projection plane ). A
two-dimensional representation of these equivalent points is then
obtained by projecting each of them onto the projection plane, with
points above the plane projecting as filled circles, and those below as
open circles.
- Symmetry elements:
The graphic in the upper right of the
window is a stereographic projection of the symmetry elements for the
chosen group. The meaning of each symbol can be found in most standard
reference texts on crystallography (ITC).
- Order: Number of symmetry operations (elements) in the group
- Notation for selected point group:
There are three different standard notations for
crystallographic point groups. The short Hermann-Mauguin symbol is most
often used, although the Schoenflies notation is commonly used as well.
An explanation of the meaning of the various group names can be found in
the ITC.
- Hermann-Mauguin (Short)
- Hermann-Mauguin (Full)
- Schoenflies
- Information about crystal system: For each crystallographic
system, there is a corresponding set of requirements for the unit cell
vector lengths and the angles between these vectors. These requirements
are specified in this section; inequality between parameters is
represented by a "<>" symbol, and any piece of information not specified
is understood to represent a free parameter.
Each of the symmetry operations for a given group are
represented as 3x3 matrices. A subset of the symmetry elements can be
used to generate all of the others; these elements are
appropriately termed generators for the group. In the Matrix
Information Window, the generators for the current group can be browsed,
and in the case of custom groups, edited.
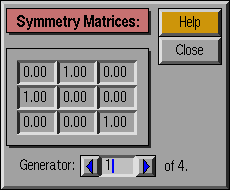
- Generator:
The number of the current generator. The total
number of generators is given to the far right. The user can jump to a
specific generator by editing the data field, or move through the
generators using the left and right arrow buttons.
- Matrix elements:
The 3x3 matrix representing a given
symmetry element. For the crystallographic and icosahedral groups, the
elements are fixed and cannot be edited; custom group elements can be changed.
The matrices of the symmetry elements for a given crystallographic group
depend on the coordinate system chosen. Facets for generating the Wulff
shape must be entered in a coordinate system that is the same as that
used to represent the symmetry elements. The default coordinate system
is Cartesian, but circumstances may arise where another coordinate
system is desirable. For example, the user may wish to enter facets in
terms of unit cell coordinates , as opposed to
Cartesian coordinates (see Figure 2).
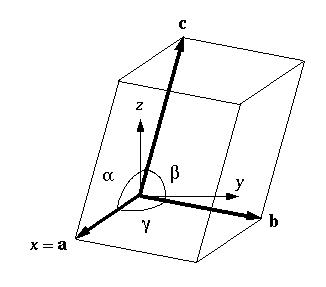
Figure 2: Unit cell parameters as defined inside Wulffman. Cell
vectors and angles are indicated. Cartesian axes are superimposed.
If facets are entered in HKL coordinates, a coordinate transformation must be
performed on the facets to change them into their appropriate Cartesian
values. The unit cell geometry for a given crystal system (cell
constants and angles as defined in Figure 2) determines the form that
this transformation takes. All of this information can be specified by
the user should such transformations be desirable. The user has the
option of either editing the values of the cell constants and angles, or
the values in the transformation matrix itself. Editing one set of
values fixes the others necessarily.
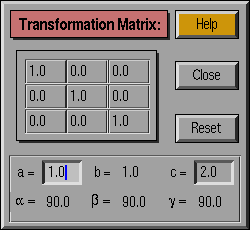
- Reset : Revert to the default transformation
- Unit cell parameters : Specify the cell parameters
for the desired transformation. The parameters that can be modified by
the user are indicated with "down" boxes, and are determined by the
current crystal system. If the crystal system is Custom, these fields
are meaningless.
- Matrix : The matrix of the transformation. This is
not editable in the case of crystallographic groups, but can be modified
for custom groups.
- Wulff Shape
- The mathematical definition of a Wulff shape is as
follows: Given a set of N planes (defined by their normals) and energies
associated with these planes {n(i),e(i)} (i=1,...,N), the Wulff
shape W is defined as
W = {r; r*n(i) <= e(i) for all i},
where r is an arbitrary point in space. Generally speaking, a
Wulff shape is the convex polyhedron that defines a minimum energy shape
for a crystal, and is hence presumably the form in which the crystal would
be observed.
- Unit cell
- The fundamental building block of a periodic crystal.
When the unit cell is repeated periodically according to the tranlsation
vectors of the crystal lattice, the entire crystal is generated.
- Group
- A group is a set that is closed under some (unspecified)
binary operation (*). Closure under this operation means that for every
pair of elements A and B in the group, the element C created by combining
A and B under this operation ( C = A * B ) must also be in the group.
There are three properties of groups:
- Every group possess an identity element I such
that for an element A, A * I = A.
- Every element A of the group possesses an
inverse A_1 such that A * A_1 = I.
- The group operation is associative, so that (A * B)
* C = A * (B * C) for elements A, B, and C in the group.
Groups are not necessarily commutative (i.e., A * B = B * A); groups
that are also commutative are called Abelian. In the above
defintion of a group, no reference is made to the properties of the
elements of the group, i.e., what these elements represent. The
simplest example of a group is a permutation group, the set of all
permutations of a collection of objects. The operation in the group is
defined as the act of permutation. The set {123, 312, 231} is a simple
permutation group of order three that is closed under a permutation that
does a simple right shift of the elements.
- Point group
- A point group is a group whose elements represent point
isometries, i.e., actions on Euclidean space that leave the distance
between points invariant. The elements of the point group leave the
environment around a point invariant. The form that these isometries
take are rotations of space, reflections through a plane, inversion
through a point, or a combination of rotation followed by inversion.
- Crystallographic Point Group
- A point group whose symmetry elements are consistent with
translationally periodic structures. Rotations in such a group are
restricted to being of order 1, 2, 3, 4 and 6. Combinations of these
rotations with reflections and inversions generate the 32
crystallographic point groups.
- Translational Periodicity
- A lattice is said to possess translational periodicity
because it can be generated by periodic repetitions of translations of a
fundamental building block, the unit cell.
- Lattice
- A collection of mathematical points in space where each
point can be written as r = a1*a + a2*a +
a3*c (a1, a2, a3 integer). Vectors a, b, and
c are referred to as the translation vectors of the
lattice, and define a nontrivial, discrete subgroup of the group of all
translations. A lattice in three dimensions is simply a set of stacked
parallelepipeds.
- Reflection / Mirror
- The symmetry operation that involves reflecting all
points through a plane. For example, if the xz-plane is taken to be a
mirror plane, then the action of this plane if to reflect every point
(x,y,z) into (x,-y,z). The type of mirror / reflection plane is defined
by its normal (i.e., the vector perpendicular to it).
- Rotation (or order n)
- The symmetry operation that rotates space about some axis
by (360/n) degrees. For example, a 4-fold rotation around the z-axis
rotates space by 90 degrees, i.e., a point (x,y,z) is rotated to (y,-x,z).
- Roto-Inversion (of order n)
- A rotation of order n followed by inversion through the
origin.
- Inversion
- The symmetry operation that takes every point (x,y,z)
into (-x,-y,-z).
- Facet
- A face of a polyhedron, defined by its normal vector.
- Order
- (i) The order of a group is the number of elements that are
contained in the group. (ii) A rotation axis of order n defines a
rotation by (360/n) degrees. (iii) The order of a group element is the
number of times that element must be applied to itself before one
obtains the identity element.
- Identity
- The element of a group that leaves elements unchanged,
i.e., A * I = A for every element A in the group. In terms of point
groups, the identity element takes every point (x,y,z) onto itself.
- Crystal system
- The classification of a three-dimensional lattice that
refers to the largest crystallographic point group that leaves the
lattice invariant. In three dimensions, there are seven such crystal
systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal
(rhombohedral) hexagonal, and cubic. The 14 Bravais lattices are a
subset of these crystal systems.
- Generator
- A group can be generated by a subset of its elements
simply by combining these elements under the group operation, thus
creating new elements. These new elements are then combined with all
elements and the process is repeated until closure of the group is
achieved.
- Stereographic Projection
- A simplified representation of equivalent points or
symmetry elements in three dimensions that involves projections of
points on the surface of the sphere onto the equatorial plane of the
sphere.
Center for Theoretical and Computational Materials Science, NIST
Questions or comments:
wulffman@ctcms.nist.gov
|
|






 WulffmanDocumentation
WulffmanDocumentation










