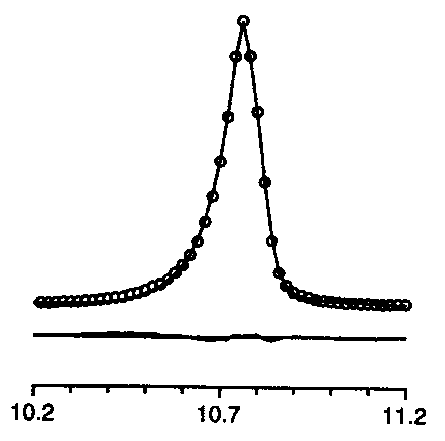
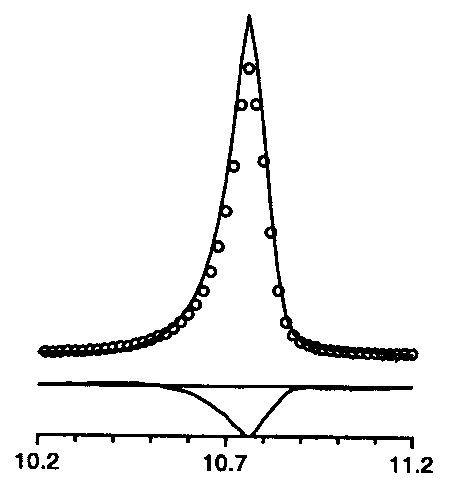
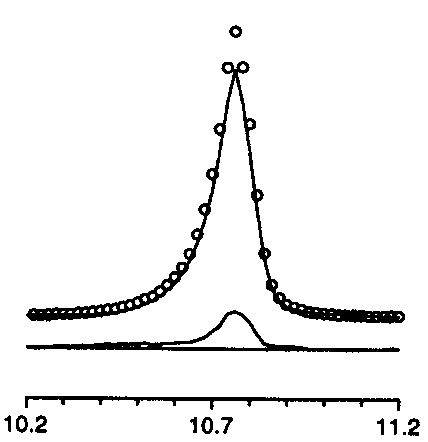
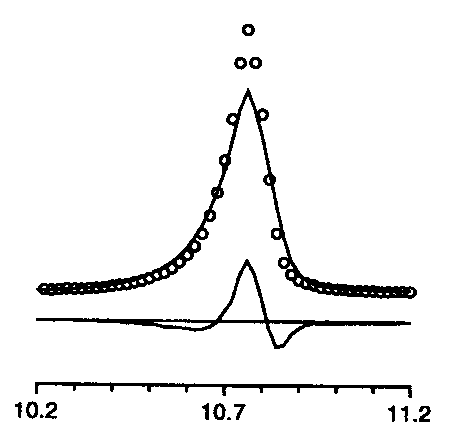
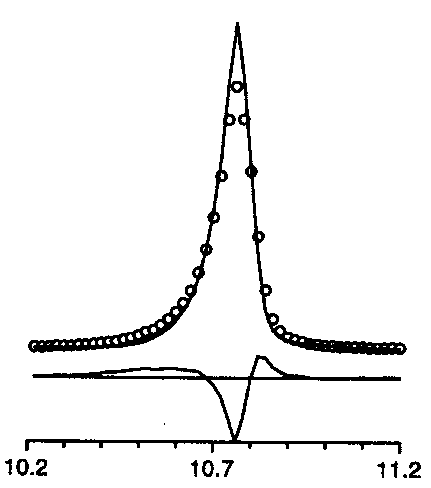
too symmetric
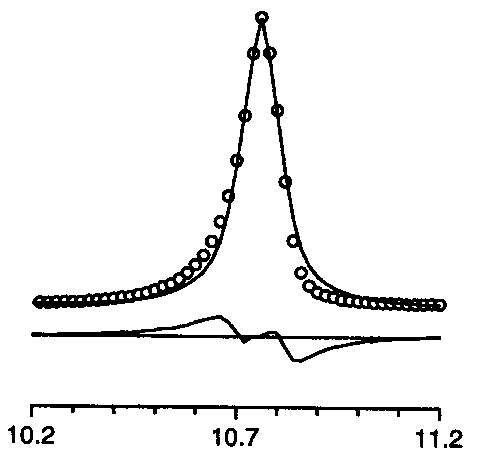
2q too large
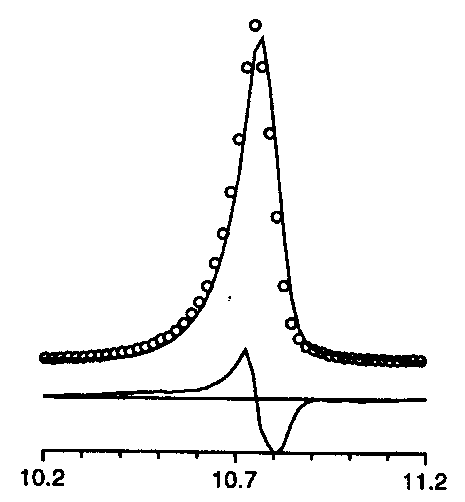
2q too small
+
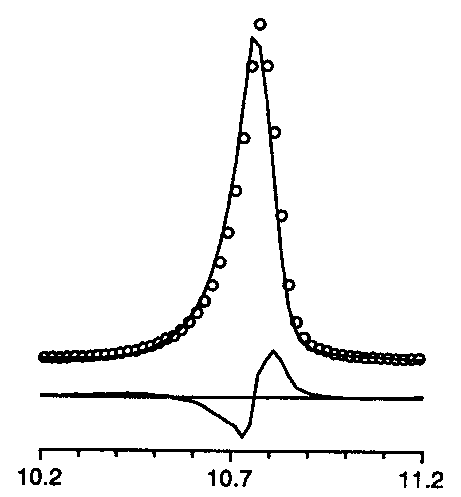
peak asymmetry too small
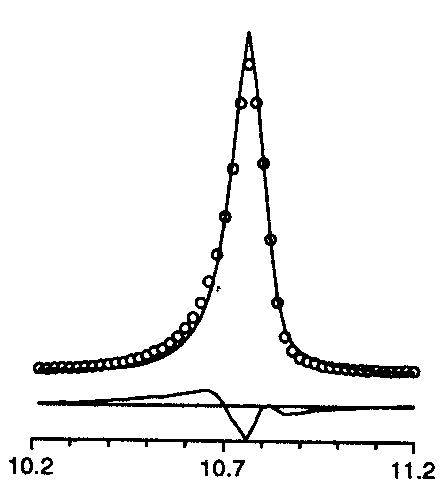
+
intensity too small
This is just a list of
selected works, essentially from
the Journal of Applied
Crystallography, and more or less classified :
The two last years appear especially rich in new theoretical developments, improvement of procedures involving material analysis by the Rietveld method.
But, remember that you
may have to use your own judgement
about their meaning.
First of all, Rietveld
refinement guidelines were formulated by the International Union of Crystallography
Commission on Powder Diffraction (McCusker et al., 1999). Having in mind
the advices given inside will help in succeeding in extracting structural
as well as microstructural details from powder diffraction data.
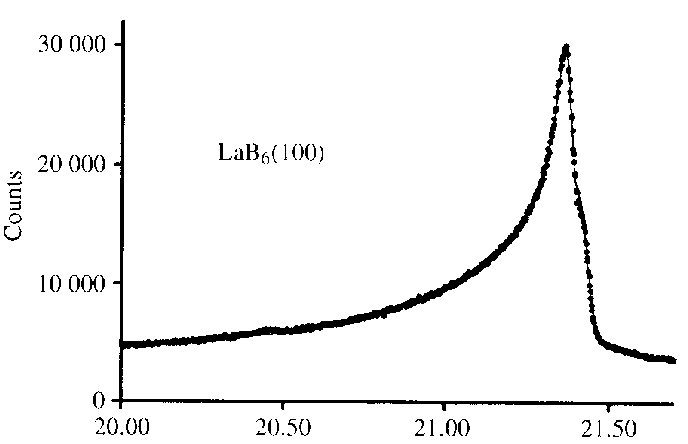
For instance, the list of characteristic effects as can be deduced from difference plots was given. Well, this is not really new, but it is useful :
|
|
 |
|
|
 |
|
|
 |
|
|
 |
|
|
 |
|
too symmetric |
 |
|
2q too large |
 |
|
2q too small |
 |
|
+ peak asymmetry too small |
 |
|
+ intensity too small |
 |
McCusker, L. B., Von Dreele,
R. B., Cox, D. E., Louër, D. & Scardi, P. (1999). J. Appl. Cryst.
32, 36-50.
A book has been published
(Microstructure Analysis by Diffraction, IUCr/Oxford University Press,
edited by Bunge, Fiala & Snyder, 1999), built mainly from contributions
to the Size-Strain'95 congress in Slovaquia. In this book, a few chapters
are devoted to microstructure analysis by using the Rietveld method
(by authors like Scardi,
Le Bail...).
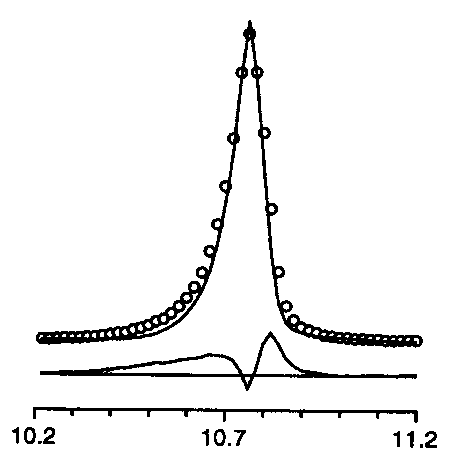
However, the microstructure
landscape, as seen from the Rietveld method, has already changed considerably.
Concerning the instrumental
profile contribution, recent advance concerns a more effective correction
of peak asymmetry due to axial divergence, since that a paper by Finger,
Cox & Jephcoat (1994) proved that this effect can be treated with parameters
related to the diffractometer optic.
A series of strongly
asymmetry affected powder patterns, including some taken on the world's
highest resolution diffractometer (at BM16, ESRF), was studied and produced
excellent fits.
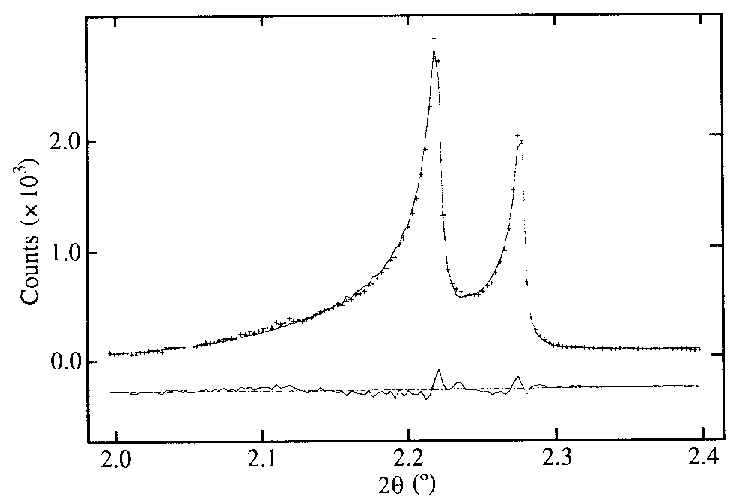
Aranda, M. A. G., Losilla,
E. R., Cabeza, A. & Bruque, S. (1998).
J. Appl. Cryst. 31, 16-21.
Equations characterizing
axial divergence in a conventional X-ray powder diffractometer were established
by Cheary and Coelho and incorporated into a fundamental-parameters convolution
synthesis and fitting program for analysing powder diffraction line profiles.
Rietveld refinement with asymmetry parameters having physical meaning is
now possible.
Cheary, R. W. & Coelho,
A. A. (1988a). J. Appl. Cryst. 31, 851-861.
Cheary, R. W. & Coelho,
A. A. (1988b). J. Appl. Cryst. 31, 862-868.
A new peak shape appeared
: a Gaussian-Hermite polynomial function for X-ray diffraction profile
fitting which can be employed in the cases where there are peak asymmetries.
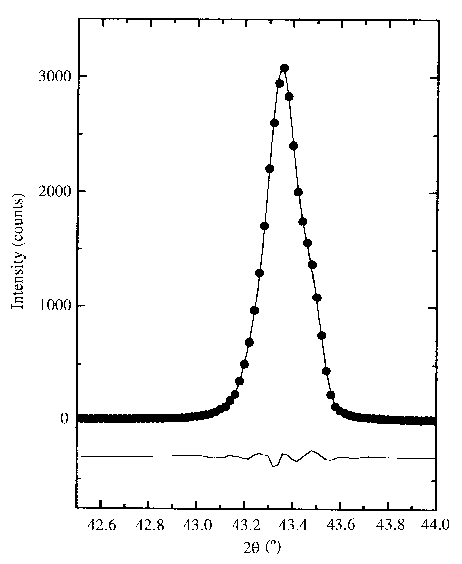
Sánchez-Bajo,
F. & Cumbrera, F. L. (1999). J. Appl. Cryst. 32, 730-735.
After a comparison of
different geometries with special attention to the usage of the Cu Ka
doublet, Oetzel and Heger recommend the use of monochromated Ka
radiation.
Oetzel, M. & Heger,
G. (1999). J. Appl. Cryst. 32, 799-807.
Many sophisticated methods
for quantitative analysis are applied within the Rietveld analysis. New
approach permits solution of the problem due to the presence of an amorphous
phase when its chemical composition is known.
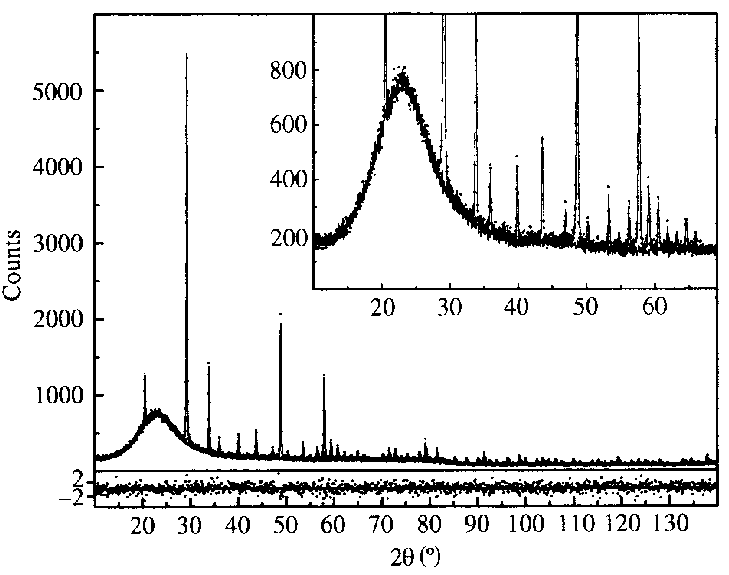
Y2O3
on amorphous silica with weight 10/90%/
Riello, P., Canton, P.
& Fagherazzi, G. (1998). J. Appl. Cryst. 31, 78-82.
More general models than simple ellipsoids were presented for the (hkl) dependence of diffraction-line broadening caused by strain and size for all Laue groups by Popa (1998). Indeed, it was proven that a quadratic form in h, k, l is too restrictive and inadequate for representing either a mean crystallite or the strain dispersion. In principle, concerning size effect, the Popa models for all Laue groups hold even if there is a contribution to the peak broadening from the stacking fault. The paper suggested that it would be possible to separate the two size effects by using a refinable faulting probability, however, equations were not provided for any symmetry. This would be quite interesting for obtaining meaningful results, and not only a phenomenological approach.
The (h,k,l)-dependent
strain models for some Laue groups :
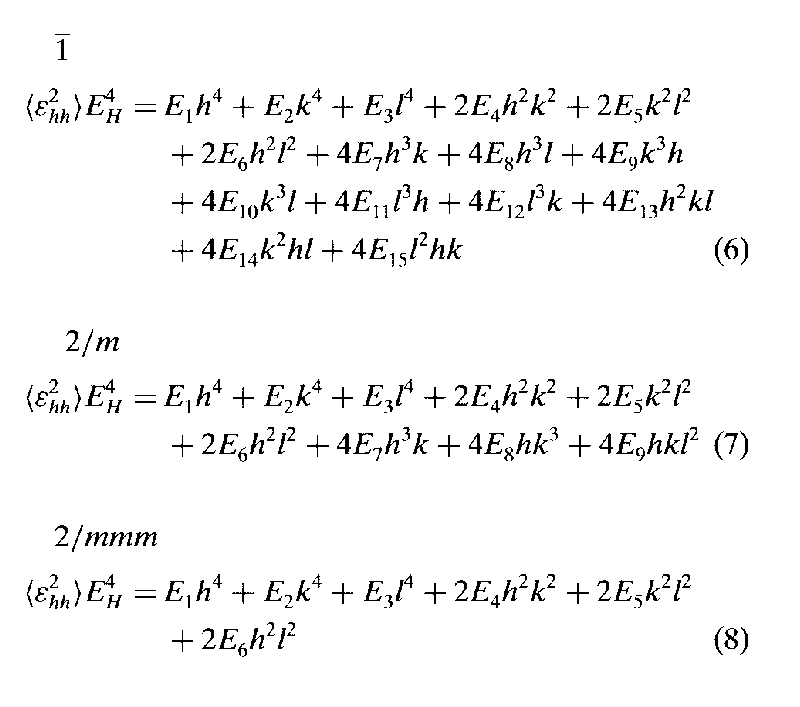
Popa, N. C. (1998). J.
Appl. Cryst. 31, 176-180.
Indeed, Stephens (1999) pointed out that, if optimal line-shape fits can be achieved in presence of anisotropic broadening, by using a model (spherical harmonic expansion) of the multidimensional distribution of lattice metrics, then microstrain parameter values cannot be predicted. The Stephens formulation of anisotropic strain broadening has been adapted into the widely-used GSAS Rietveld method package (Larson & Von Dreele, 1994). Stephens equations are more restrictive than Popa's ones, as justified by exact overlapping of reflections for some Laue class which would not allow to extract distinct parameters from powder data.
The phenomenological model
of anisotropic strain broadening, proposed by Stephens, considers the distribution
of lattice metric parameters within a sample. Each crystallite is regarded
as having its own lattice parameters, with a multi-dimensional distribution
throughout the powder sample. It is a generalized approach deriving from
previous similar but more restrictive descriptions, already included in
FULLPROF for instance. In the case of this sodium para-hydroxy benzoate,
the reliability factor decreased from fifteen to eight percent.
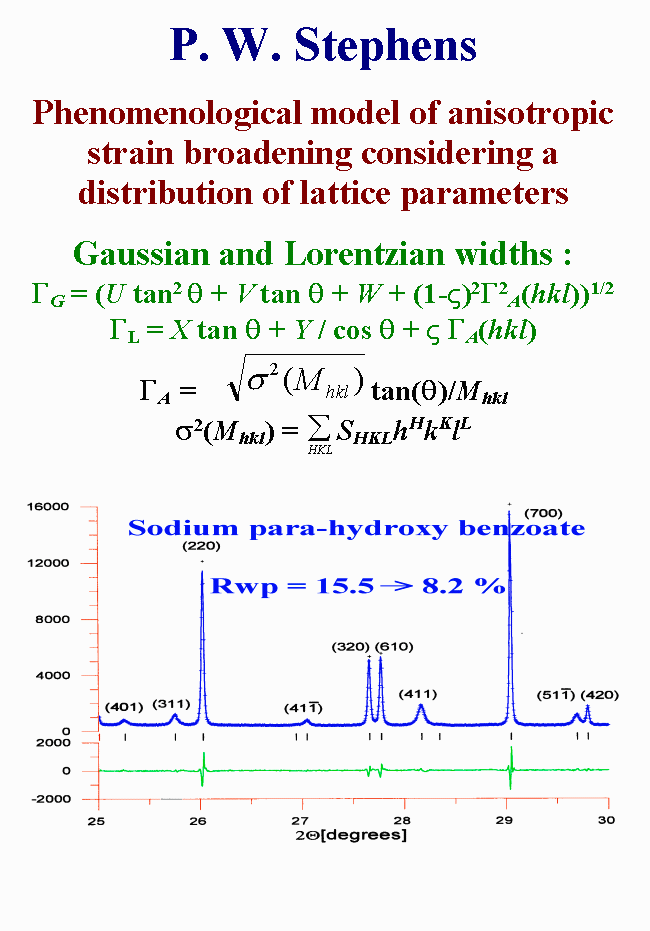
Stephens, P. W. (1999).
J. Appl. Cryst. 32, 281-289.
More details were published
later, with the ab initio structure solution of sodium para-hydroxybenzoate
: estimation of the strain distribution. The meaning of that curious shape
is not well understood... The question should be reserved to the Sphinx
?
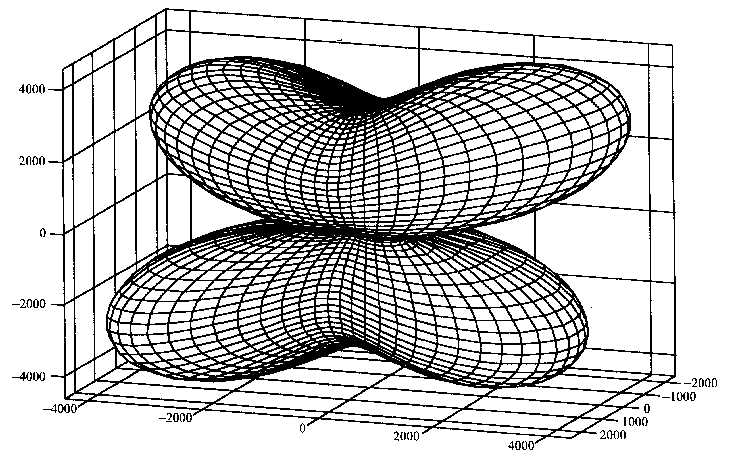
Dinnebier, R. E., Von Dreele, R., Stephens, P. W., Jelonek, S. & Sieler, J. (1999). J. Appl. Cryst. 32, 761-769.