Trying to add some physically sound bases to those phenomenological models, Ungár, Leoni and Scardi (1998) applied the dislocation-based model of strain anisotropy in the Fourier formalism of profile fitting. A perfect profile fitting to the powder pattern of a Li-Mn spinel was enable from a few physically sound parameters, namely the average dislocation density, the average coherent domain size, the dislocation arrangement parameter and the dislocation contrast factor.
Cubic spinel sample :
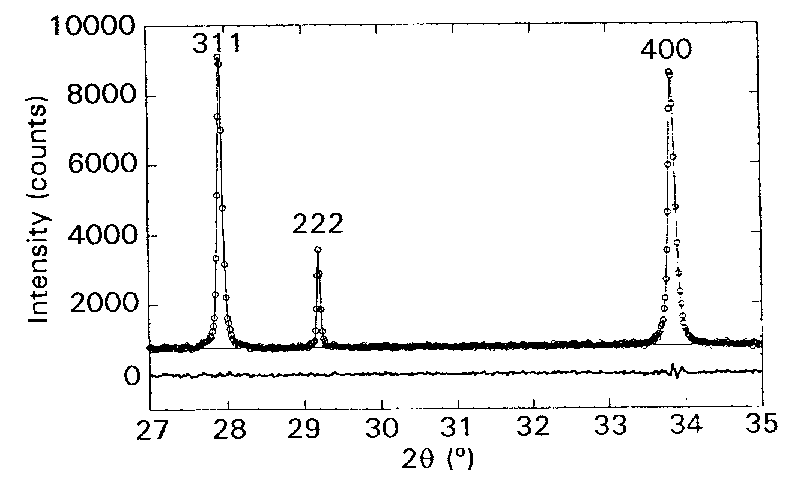
Ungár, T., Leoni,
M. & Scardi, P. (1998). J. Appl. Cryst. 32, 290-295.
Anisotropic line broadening
of X-ray diffraction profiles due to line and plane lattice defects was
also said to be Fourier modelled (Scardi & Leoni, 1999). Applications
to face-centred cubic structure materials provided detailed information
on the defect structure : dislocation density and cut-off radius, stacking-
and twin-fault probabilities were refined together with the structural
parameters.
Cu-tablet. Mixed
model, dislocations + stacking and twin faults :
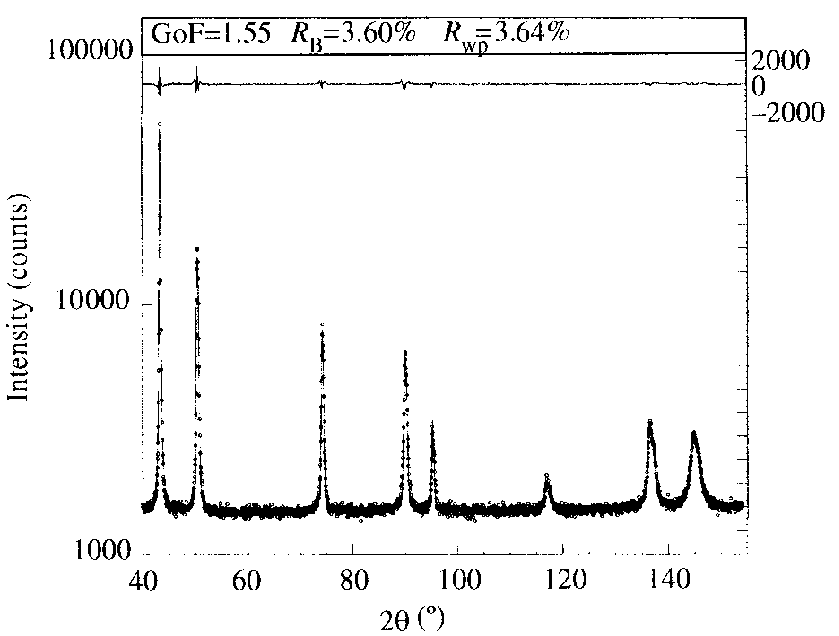
Scardi, P. & Leoni,
M. (1999). J. Appl. Cryst. 32, 671-682.
A simple procedure for
the experimental determination of the average contrast factor of dislocations
has been established. The character of the dislocations can be determine
in terms of a simple parameter q which can be used in Rietveld structure
refinement procedures.
Ungár, T., Dragomir,
I., Révéz, Á & Borbély, A. (1999). J. Appl.
Cryst. 32, 992-1002.
Size-effect only is much
easier to consider than both size-microstrain. How being sure that only
a size effect occurs ? This could be shown by transmission electron micrograph
of the powder. Then, the size distribution of single-crystal nanoparticles
can be estimated by different approaches. One approach consists in Monte
Carlo fitting of wide-angle X-ray scattering peak shape (Di Nunzio &
Martelli, 1999). Another method applies maximum entropy for determining
the column-length distributions from size-broadened diffraction profiles
(Armstrong & Kalceff, 1999) as well as for removing instrument broadening.
Di Nunzio, P. E. &
Martelli, S. (1999). J. Appl. Cryst. 32, 546-548.
Armstrong, N. & Kalceff,
W. (1999). J. Appl. Cryst. 32, 600-613.
Dislocations are at the hearth of microstrain effects.
Many studies are undertaken in order to describe dislocations scattering effects.
If dislocations are described
by statistical effects in powder diffraction, such an approach may prove
soon to be oversimplified. More accurate description of dislocations may
be required in order to access to more accuracy in the diffraction pattern
simulation.
Synchrotron topography
technique, simulation of micropipe-related superscrew dislocations in silicon
carbide crystals, allowed to build a model capable of revealing the detailed
diffraction behavior of the highly distorted region around the dislocation
core (Huang et al., 1999). Considering that the distorted regions consist
of small misoriented crystallites which diffract X-rays kinematically according
to their local lattice orientation, they have developed a simplified numerical
model for simulating the direct images of superscrew dislocations in synchrotron
topographs.
Huang, X. R., Dudley,
M., Vetter, W. M., Huang, W., Si, W. & Carter Jr., C. H. (1999). J.
Appl. Cryst. 32, 516-524.
The theory of dislocation-induced
X-ray or neutron diffraction line broadening has been adapted for Rietveld
refinement by fitting a Voigt function to each peak (Wu, Gray & Kisi,
1998). Information on both the type of slip system and the density of dislocations
in the crystallites may then be found by evaluating the shape parameter
and the index-dependent breadth of the Voigt function. Precise description
of the dislocation model seems to be possible by using this method. Applications
(Wu, Kisi & Gray, 1998) were on deuterium-cycled LaNi5 and
b-PdD0.66
neutron powder diffraction data.
Wu, E., Gray, E. Mac
A. & Kisi, E. H. (1998). J. Appl. Cryst. 31, 356-362.
Wu, E., Kisi, E. H. &
Gray, E. Mac A. (1998). J. Appl. Cryst. 31, 363-368.
X-ray scattering by crystals
with local lattice rotation fields was examined by Barabash and Klimanek
(1999). The peculiarities of the intensity distribution is dependent on
the dislocation arrangements.
Barabash, R. I. &
Klimanek P. (1999). J. Appl. Cryst. 32, 1050-1059.
What to do when a material is highly disordered and a space group cannot be defined so that the Rietveld method cannot be utilized directly ? An answer was given by Schilling and Dahn (1988) who fitted complex patterns of disordered manganese dioxides. In their paper, the g-MnO2 structure is defined as an intergrowth of ramsdellitic and pyrolusitic domains. They proposed an analytic expression for the scattered intensity calculated from a stochastic stacking of four different types of layers.
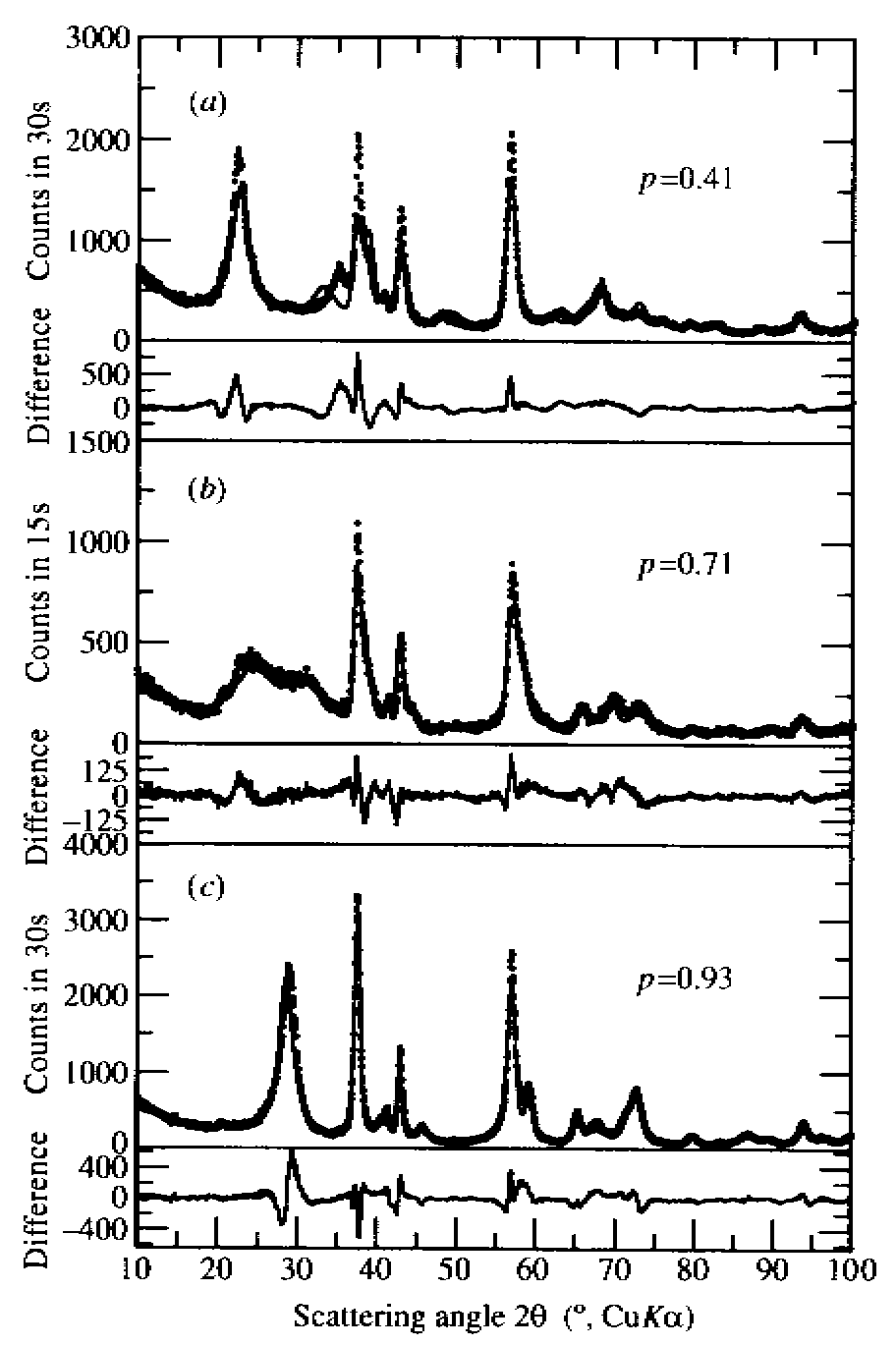
Schilling, O. & Dahn,
J. R. (1998). J. Appl. Cryst. 31, 396-406.
Convoluting or deconvoluting
is a choice to be made at the beginning of a study of microstructures.
Either the instrumental contribution is convoluted with the sample effect
in order to regenerate the raw powder pattern, or a deconvoluted could
be performed for extracting the sample contribution. The latter option
is still not in use due to non preservation of intensity positivity and
presence of spurious oscillations in the deconvoluted profile. One can
note also that the separation of the Ka1
component from Ka2
is not at all recommended for analogous reasons (sometimes improperly described
as a deconvolution instead of decomposition or desummation).
Armstrong, N. & Kalceff,
W. (1998). J. Appl. Cryst. 31, 453-460.
However, deconvolution
has to be done and the Fourier coefficients of the individual profile are
needed if one wants to realize a Warren and Averbach (1950) analysis.
When possible, this is
the best to do as was done in the study of dislocations and grain size
in electrodeposited nanocrystalline Ni (Ungár, Révéz
& Borbély, 1998), applying too the Williamson and Hall (1953)
plot. The Scherrer particle size continues to be estimated with assumption
of spherical particles (Klug & Alexander, 1974), for instance in the
investigation of germanium nanoclusters (Bläsing et al., 1998). A
recent tool (AXES software) for estimation of crystallite size and shape
by Williamson-Hall analysis was proposed by Mändar et al. (1999).
Ungár, T., Révéz,
Á & Borbély, A. (1998). J. Appl. Cryst. 31, 554-558.
Bläsing, J. Kohlert,
P., Zacharias, M. & Veit, P. (1998). J. Appl. Cryst. 31, 589-593.
Mändar, H., Felsche,
J., Mikli, V. & Vajakas, T. (1999). J. Appl. Cryst. 32, 345-350. AXES
is available electronically at http://www.ccp14.ac.uk/.
Recent applications include
the microstructural investigation of plastically deformed Pb(1-x)Snx
alloys through a profile fitting approach within the framework of the Warren-Averbach
and the Williamson-Hall methods.
Chatterjee, P. &
Sen Gupta, S. P. (1999). J. Appl. Cryst. 32, 1060-1068.
When even more disorder
is detected, using variants of the Rietveld method has proved to be useful.
Application to the characterization of disordered and small crystals
as found in semicrystalline polymers was recently published (Dupont, Jonas
& Legras, 1997). The possible tilt angle of chain axes versus the large
faces of the lamellar crystals were introduced in the model of PEEK [poly(ether-ether-ketone)]
(Dupont et al. 1999). However, models with or without chain tilt give similar
goodness-of-fit parameters, indicating that results coming from other techniques
than X-ray diffractometry are required in order to characterize the dimensions
and shape of crystals in isotropic polymer samples.
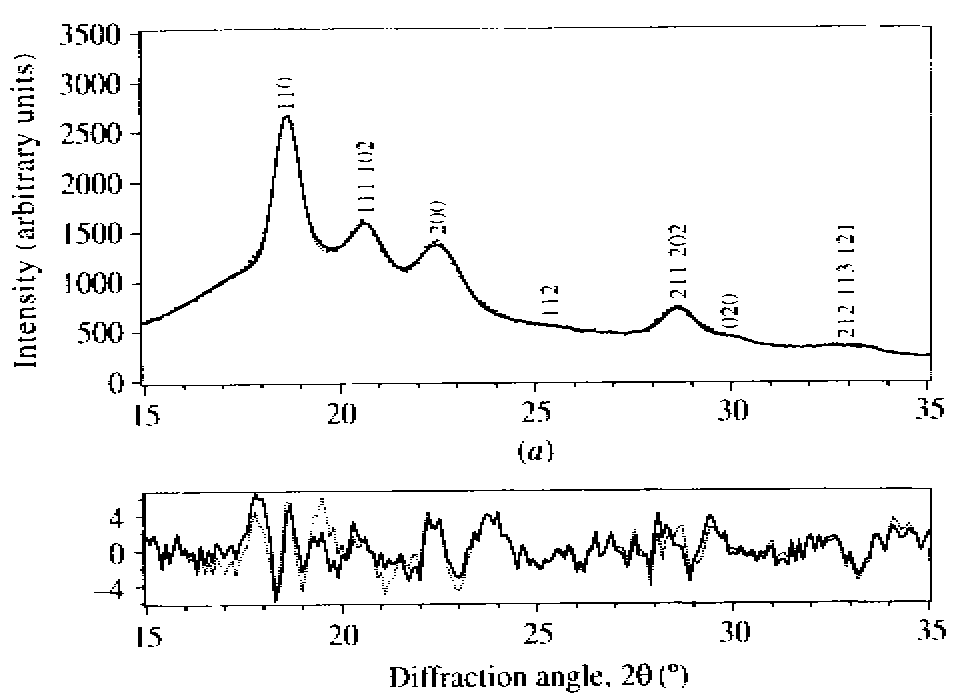
Dupont, O., Jonas, A.
M. & Legras, R. (1997). J. Appl. Cryst. 30, 921-931.
Dupont, O., Ivanov, D.
A., Jonas, A. M. & Legras, R. (1999). J. Appl. Cryst. 32, 497-504.
Studying 10 and 8.4 Å
hydrates of kaolinite proves to be still difficult, if one looks at the
best fits (not Rietveld) obtained by Jemai (1999).
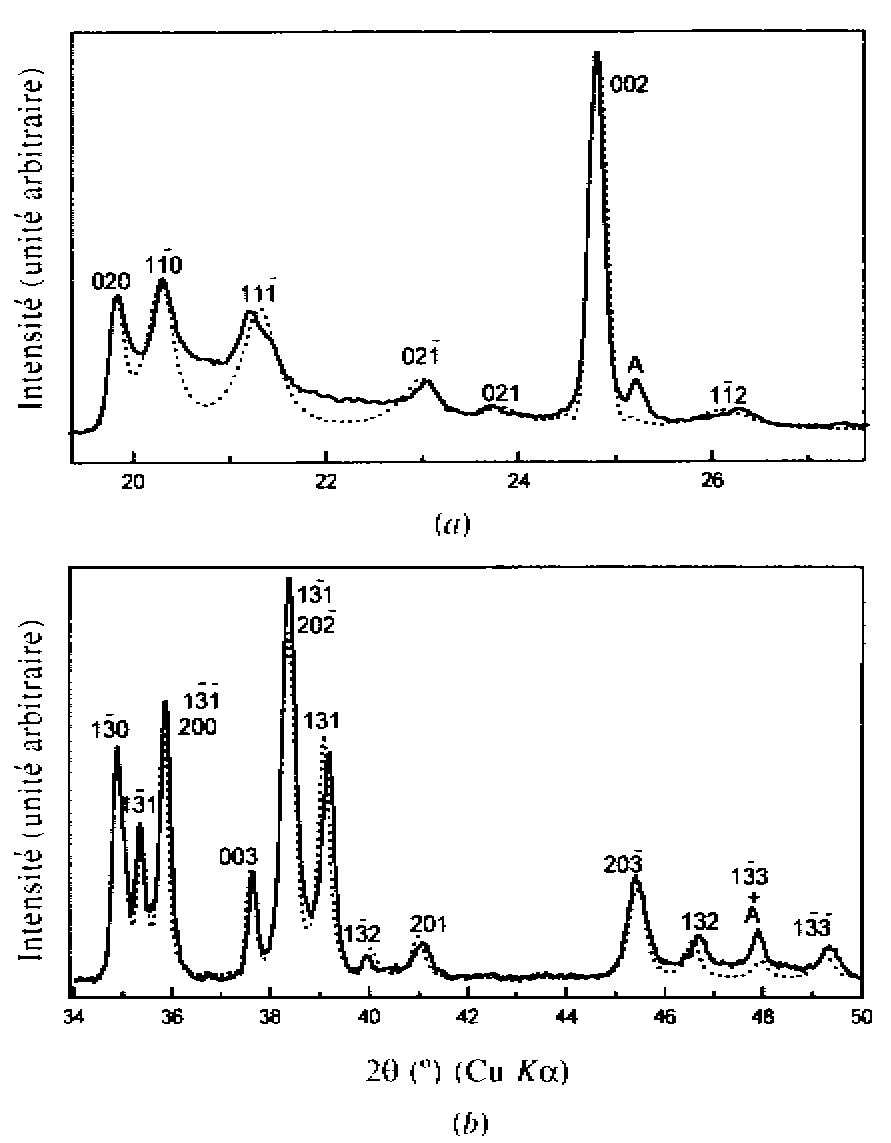
Kaolinite
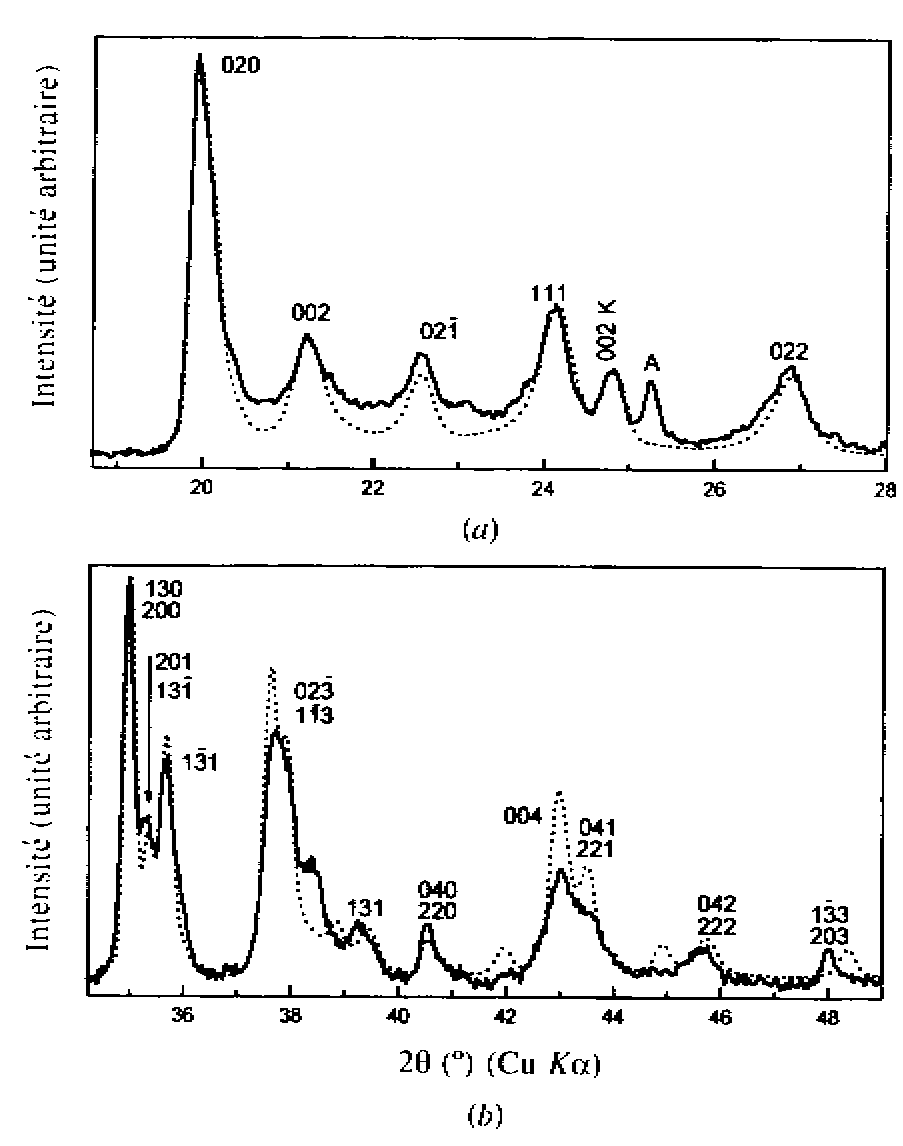
Hydrate 8.4 A
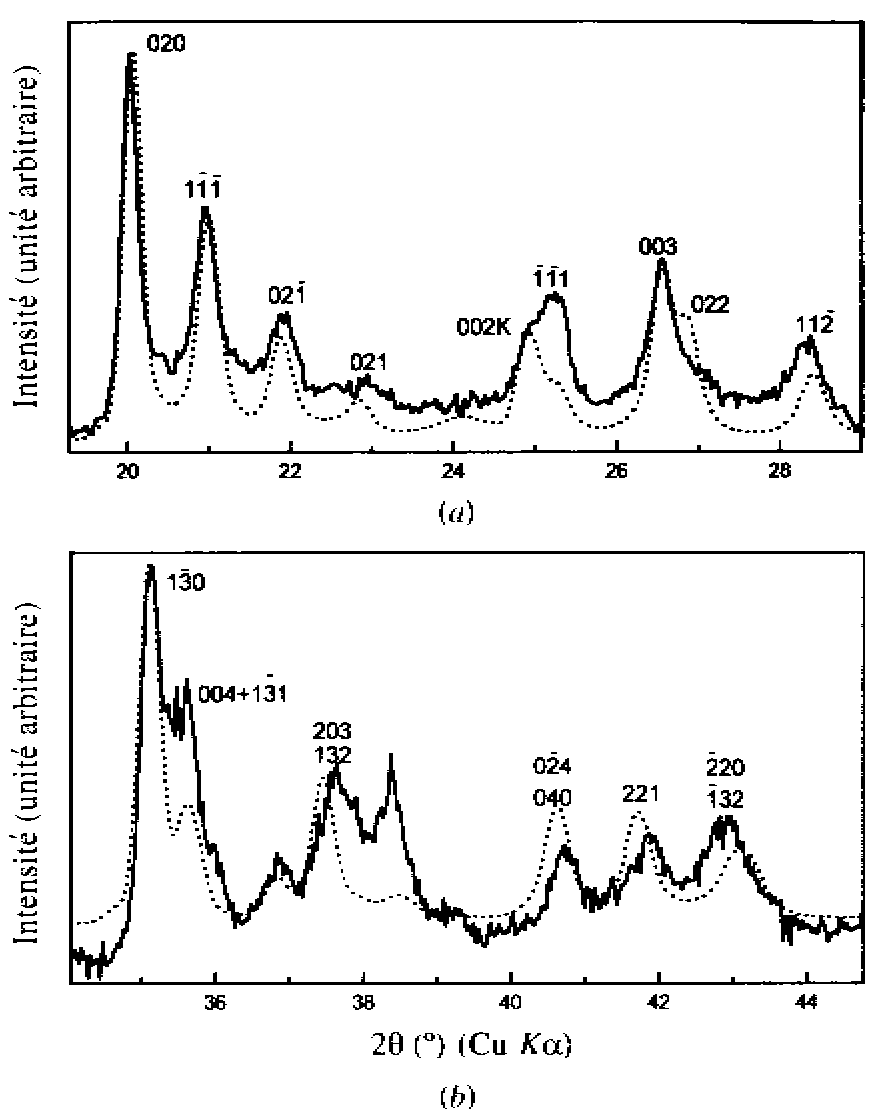
Hydrate 10 A
Jemai, S., Ben Haj Amara,
A., Ben Brahim, J. & Plançon, A. (1999). J. Appl. Cryst. 32,
968-976.
The effect of sample transparency
in powder diffractometry is generally treated in the Rietveld method by
a simple peak displacing law. Ida and Kimura (1999a) treat this effect
for Bragg-Brentano geometry as a convolution with an asymmetric aberration
function. Also, they show that the flat-specimen effect on the peak profile
can quantitatively be treated as a convolution with an asymmetric window
function (Ida & Kimura, 1999b).
Ida, T. & Kimura,
K. (1999a). J. Appl. Cryst. 32, 982-991.
Ida, T. & Kimura,
K. (1999b). J. Appl. Cryst. 32, 634-640.
Additional references