The defects induced by hydrogen absorption and desorption in the lanthanum-nickel compound were recently observed by Transmission-Electron-Microscopy, allowing to suggest what exactly is behind those mysterious root mean square strain and mean apparent size values estimated from powder data. The electron-microscopy study evidenced many kind of dislocations (ripple-like, fence-like, misfits, and loops), also anti-phase boundaries, fracture of slip band structure, structural disorder and micro-twins. All these defects have effects on the powder pattern that are gathered in those size and microstrain values. Progress and innovations in microstructure analysis by the Rietveld method will never overcome this fact : the powder pattern reveals the whole problem at a one-dimensional scale, and as a mean.

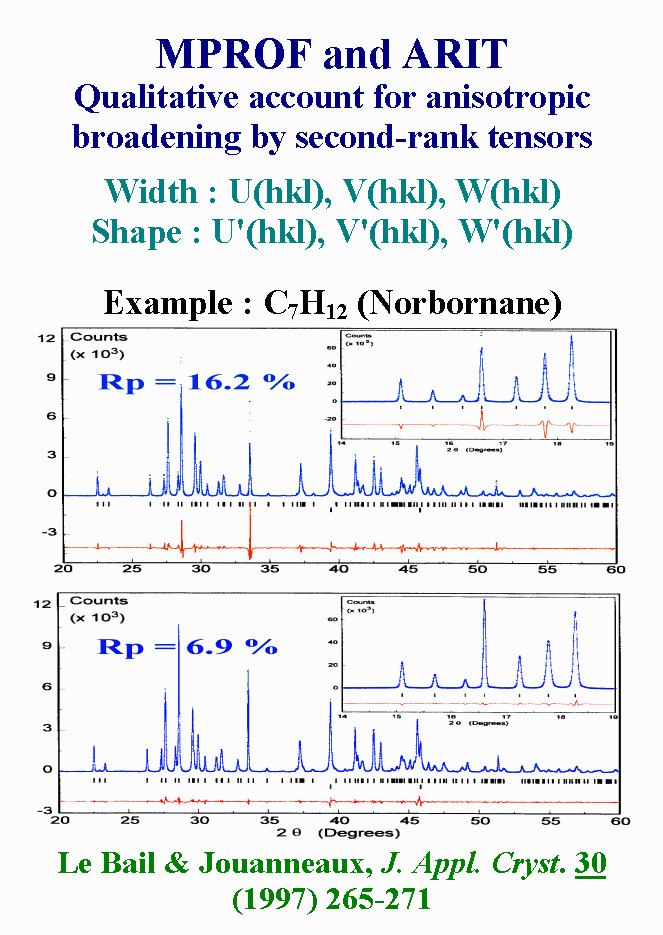
The trend to deal qualitatively with microstructure effects is illustrated with the case of Norbornane. Fitting with isotropic line broadening was a kind of disaster. The synchrotron powder pattern was then fitted with the MPROF Rietveld program, using empirical simulation of anisotropic line broadening. In this approach, each usual U, V, and W parameters which describe the peak width and also the peak shape angular variation, was made hkl-dependent through second-rank tensors, leading to thirty-six variables maximum in the triclinic case. The R_P value was lowered by almost a factor 2.

 
 
 
 
 
 
 

Let us now examine some complex cases by using one of the most recent Rietveld programs. BGMN is a commercial package, that is able to behave as an expert system in a few predefined cases, including stacking faults in disordered layer silicates. It works by using a Fundamental Parameter Approach for the instrumental profile. About size-microstrain effects, BGMN uses Lorentzian broadening (for crystallite size) and squared Lorentzian broadening (for microstrain). 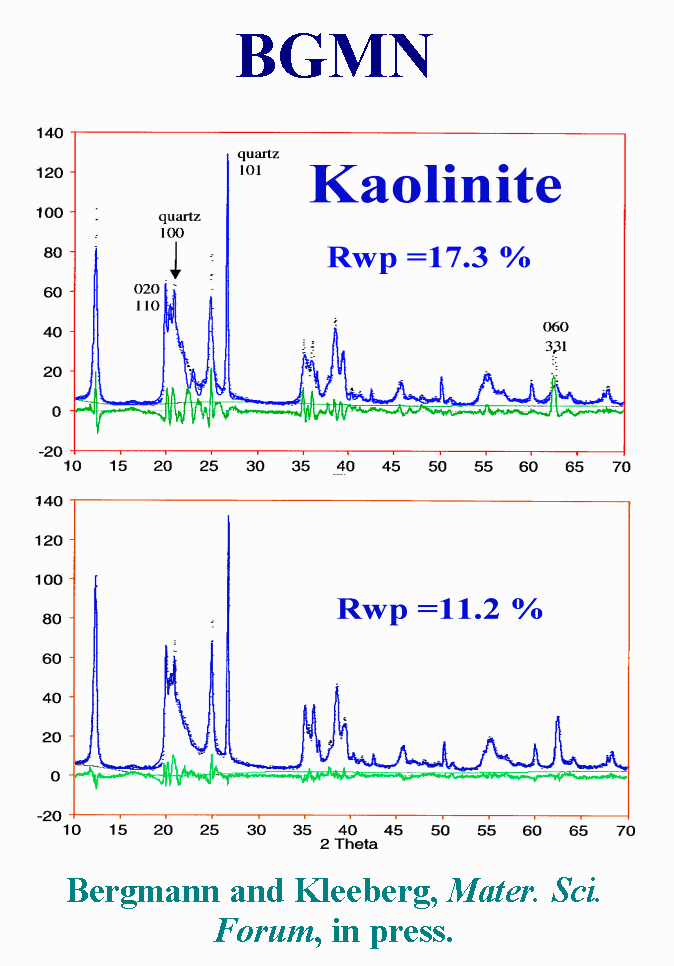BGMN has default dependence from size/strain. But you may select arbitrary other dependencies using the built in formula interpreter. This is what was done for kaolin by introducing a model of disordering : essentially the pattern is decomposed in 3 sub-phases with different broadening laws. Yes the fit is improved, but I have not found any size or microstrain or probability of stacking fault values in the published paper.

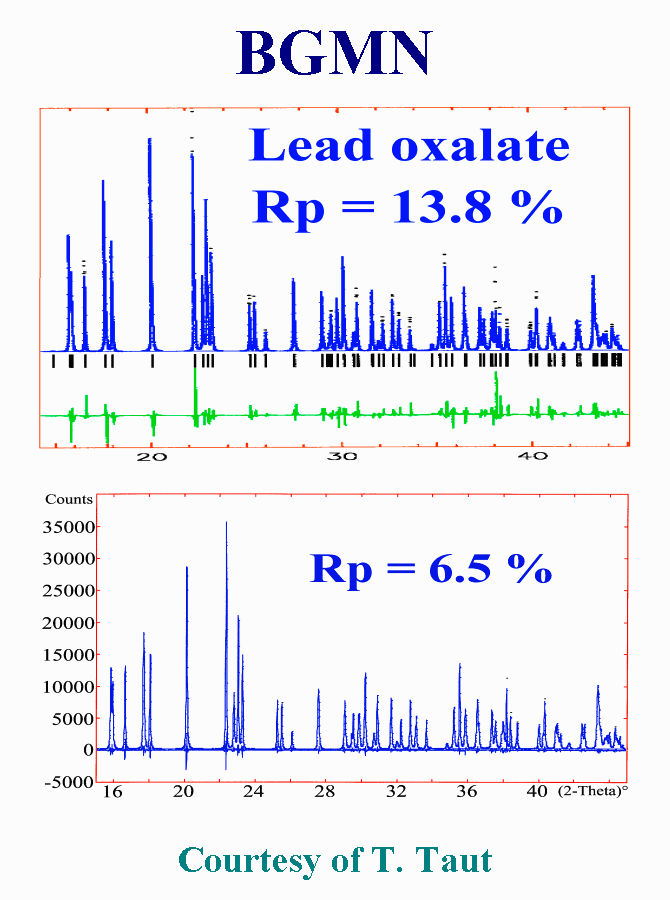
I asked Thomas Taut for some tests on my two favourite ill-crystallized samples with BGMN. One is lead oxalate of which the synchrotron pattern is hard to fit due to stacking faults. BGMN uses ellipsoids as a possibility for anisotropic effects, but this allowed to decrease the Rp value only by 2 %. Assuming that there were two slightly different real structures of the same phase, with nearly the same lattice constants but different peak broadening considerably improved the fit by BGMN with R_P = 6.5 %. The approach is only qualitative but shows the ease of use of BGMN. In fact the fit was without the structure constraint, using the Le Bail method I guess, and could not be realized with the simultaneous refinement of the atomic coordinates.

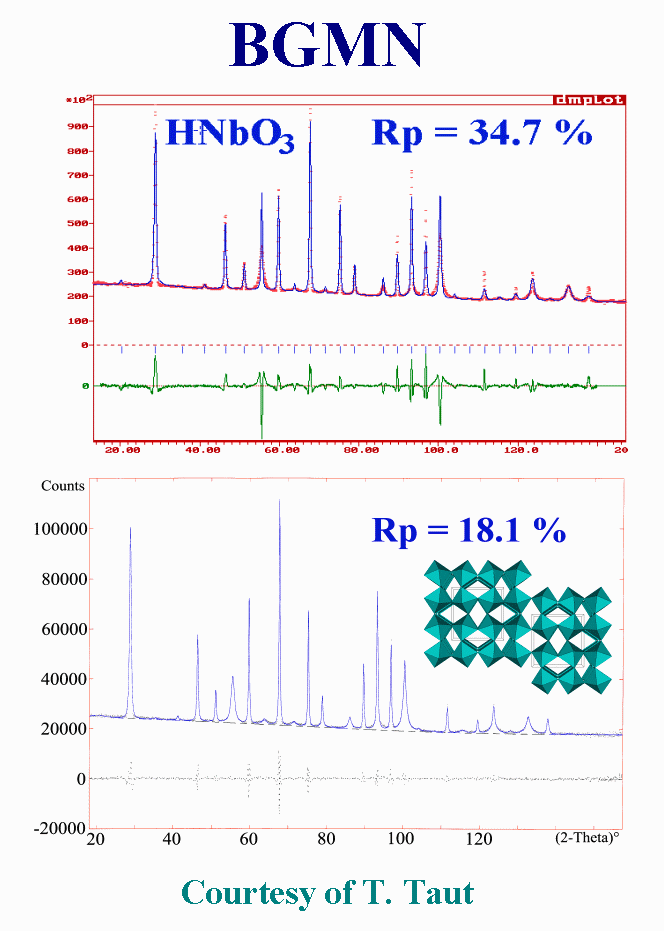
Another highly problematic powder pattern of a hydrogen niobium oxide was treated with BGMN in a similar way, using two subphases with different peak broadening, but with less success, the reliability R_P value decreasing from thirty-five to eighteen percent, which is rather still high. Moreover, because the individual intensities are arbitrary distributed over the two "phases", introducing the structure constraint on intensities may alter considerably the fit quality. Both samples and patterns are challenges for the proposition of a physically sound model that would allow a satisfying fit by the Rietveld method, including the structure refinement. The perovskite-type niobium compound is very probably affected by anti-phase domains extending in the three dimensions as suggested by this picture.