Breaking the phase ambiguity in protein crystallography
The philosophy is that, the
phase ambiguity is first converted to a sign ambiguity, the latter is then
resolved by a direct method. This was proposed in the 1960's [Fan Hai-fu,
Acta
Phys. Sin. (1965) 21, 1114-1118 (in Chinese). See also Fan,
H.F.,
Chinese Physics (1965) 1429-1435
![]() ]. Further development has
been carried out from 1983 till now.
]. Further development has
been carried out from 1983 till now.
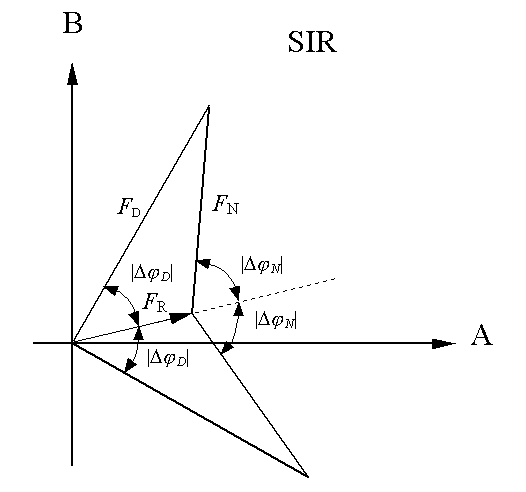
In SIR case, for a given reciprocal-lattice vector h, we have the structure-factor relation
![]() . (1)
. (1)
Here the subscript N, D and R denotes respectively the native protein, the derivative and the replacing-atom substructure. From experiment we know the magnitude of F(h,D) and F(h,N). Hence we can find the position of the replacing atoms and calculate the vector F(h,R). Then we have two different ways to draw the triangle of equation (1) leading to an enantiomorphous phase doublet for F(h,D) and for F(h,N) as in the following figure.
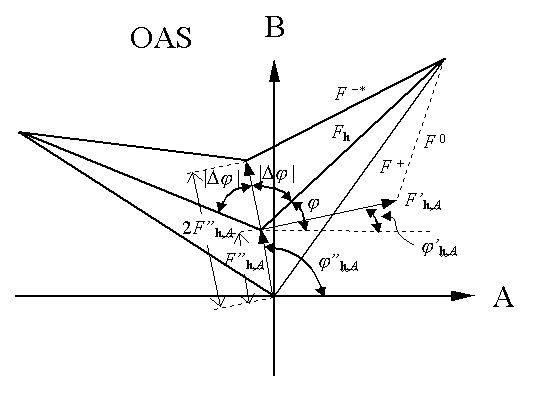
In OAS case on the other hand, we have
![]() (2)
(2)
The magnitude of F(+h) and F*(–h) can be obtained from experiment, while F"(h,A) can be derived from the known anomalous-scatterer substructure. Hence we have also two ways to draw the triangle of equation (2) leading to an enantiomorphous phase doublet for F(h) as shown below
To summarize, the phase doublet in both SIR and OAS cases can be expressed as
![]() . (3)
. (3)
The problem of splitting enantiomorphous phase doublets is that of
finding the sign of ![]() ,
given the known values of
,
given the known values of ![]() and
and ![]() .
.
For SIR case we have ![]() and
and ![]() when we are deriving phases for the native protein, or
when we are deriving phases for the native protein, or ![]() when phases are derived for the derivative.
when phases are derived for the derivative.
For OAS case we have ![]() and the phases are derived for
and the phases are derived for ![]() .
.
In order to break the phase
ambiguity, a tangent formula among ![]() and the probability for
and the probability for ![]() to be positive have been worked out [Fan & Gu, (1985). Acta Cryst. A41,
280-284
to be positive have been worked out [Fan & Gu, (1985). Acta Cryst. A41,
280-284 ![]() ]:
]:
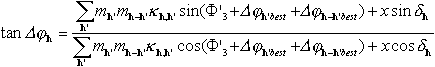 (4)
(4)
![]()
![]() . (5)
. (5)
Here
![]()
![]() , Zj is the atomic number of the jth atom in the unit cell;
, Zj is the atomic number of the jth atom in the unit cell;
![]() ;
;
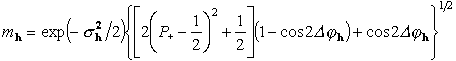 ; (6)
; (6)
![]() ;
;
![]() ; (7)
; (7)
![]() ,
Eh, p is the contribution of the known partial structure (replacing atoms or anomalous scatterers) to the magnitude of normalized strructure factor;
,
Eh, p is the contribution of the known partial structure (replacing atoms or anomalous scatterers) to the magnitude of normalized strructure factor;
![]() ,
Zu is the atomic number of the uth atom belonging to the unknown part of the unit cell;
,
Zu is the atomic number of the uth atom belonging to the unknown part of the unit cell;
![]() ,
,
![]() is the phase of Eh, p.
is the phase of Eh, p.
At start, equations (6) and (7) are used with P+ = 1/2. The results are substituted into (5) to obtain a new set of P+.This
is fedback to (6), (7) and then to (5). Usually two cycles will be enough
for breaking the sign ambiguity of ![]() .
A program OASIS
has been written in Fortran for the above calculation.
.
A program OASIS
has been written in Fortran for the above calculation.
Equation (4) is an enantiomorph-sensitive
tangent formula, it may be useful for refining the sign as well as the
magnitude of ![]() .
Practical applications of equation (4) is still to be explored.
.
Practical applications of equation (4) is still to be explored.