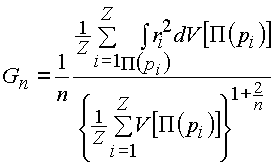 ,
(1)
,
(1)Z. Kristallogr. 1998. V.213, N 4. P.202-209.
Analysis of environment of alkali atoms in oxygen-containing compounds with Voronoi-Dirichlet polyhedra
V.A.Blatov, L.V.Pogildyakova and V.N.Serezhkin
Samara State University, Ac. Pavlov St. 1, 443011 Samara, Russia
E-mail: blatov@ssu.samara.ru
Voronoi-Dirichlet polyhedron / Alkali atom / Atomic volume / Coordination number
Abstract. It is shown that coordination numbers (CN) of alkali atoms can be determined in crystal structures by means of Voronoi-Dirichlet polyhedra without using crystal-chemical radii. It is found that a domain with constant volume corresponds to an alkali atom at CN� 6. The conclusion about correctness of application of the model of deformable spheres for the description of alkali atoms in a crystal field is drawn.
Introduction
The hypothesis of constancy of atomic volume in crystals, which is a natural development of the concept of atomic radii, is long known in crystal chemistry [1]. At the same time, the problem of selection of atomic domains, strict decision of which requires the use of complex methods of quantum mechanics [2] or of the precise structural experiment [3], allows one to examine the above-mentioned hypothesis only for structures of simple compounds. In this case, the atomic domain is well approximated by Voronoi-Dirichlet polyhedron (VDP). Recently was shown [4] that VDPs can be successfully used for an estimation of domains of the complexing atoms which have only chemically identical atoms in the first coordination sphere. It was found for oxygen- and fluorine-containing compounds of U(II-VI) and Zr(IV) [4-6] that the hypothesis of constancy of atomic volume can be correct also for structures of complex compounds under the condition of conservation of the electron state of an atom. Since the coordination numbers (CN) of alkali atoms (M) in crystal structures vary in a wide range (according to [7], from 4 to 14), it would be interesting to verify the hypothesis of constancy of the dimensions of these atoms for the most numerous oxygen-containing compounds.
Experimental
Data collection
For the investigation a database covering the information on structure of about 1500 compounds of alkali atoms which contain coordination polyhedra MOn was created by means of the TOPOS program package [4]. VDPs were constructed through the DIRICHLET program included in TOPOS. The information on structures was put into the database with respect to the following conditions:
- the structural determination was executed with Rf
�10%;- according to the description of a structure given by the authors, it contains alkali atoms, whose environment consists of only oxygen atoms;
- the structure does not contain alkali atoms and/or oxygen atoms which are statistically distributed on crystallographic positions.
The method of determination of coordination numbers
Firstly, let us note that for the examination of the effect of volume invariance for atomic domains of alkali atoms it is necessary to solve the problem of CN determination. Usually, the description of crystal structure is restricted by the indication of values of interatomic distances R(M-L) (L is the donor atom of a ligand) in some range, the upper value of a range is defined as a sum of ionic radii r(M)+r(L), which is frequently outspread on 0.3-0.4µ. Obviously, when R(M-L) values change in a wide range and the coordination sphere of M atom is ‘diffuse’, the method described becomes only formal. As a rule, namely this case is typical for alkali atoms (r(M+)+r(O2-)=1.94 to 3.30µ depending on CNs of M and O atoms and on the nature of M atoms [7]), that requires the new methods of an estimation of their CNs. In this study for determination of CNs of M atoms we use VDPs, the number of whose faces allows one to determine CNs of corresponding atoms [8]. However, it is necessary to take into account that each face of VDP does not always correspond to a strong (ionic, covalent or metallic) chemical bond [4-6]. Therefore, during the estimation of atomic CNs by means of VDPs one has to take into consideration the following:
1. According to [4], the strength of interatomic bond is proportional to the value of solid angle (
W ) of the face which is joint for VDPs of considered atoms. Obviously, when W values do not exceed the standard deviation caused by errors of structural experiment (s(W )� 1.5% of the total solid angle of 4p steradian), there are no reasons to speak about presence of strong interatomic interactions, and corresponding faces of VDP should not be taken into account.2. A certain face of VDP of M atom can correspond to the so-called ‘indirect’ neighbour [9], i.e. to the L atom, for which the centre of M-L segment does not lie on VDP surface. In this case, according to [9], M-L contact should not be considered as a chemical bond.
3. It is necessary to clarify whether a set of interatomic interactions, to which the faces of VDPs with
W >1.5% correspond, is identical and whether it is required to make their additional classification before the final CN calculation. In this case, the total atomic CN can be written as Sni, where ni shows the number of interatomic contacts of identical (or almost identical) nature, and index i=1 to m enumerates m different types of interatomic interactions in order of decreasing their strength. Note that, usually, CN=nl is assumed independently of the range of i. Further we shall call so-defined CN as classical (CNcl), and use the abbreviation ‘CN’ for designation of total CN.From the remarks indicated the first two are formalised and can be easily taken into account during the determination of CNs, whereas the classification of interatomic interactions seems to be a rather complex methodological problem. For the illustration of our proposed method of decision of this problem, we shall consider distributions of R(M-O) and corresponding
W (M-O) in VDPs of M atoms.Results and discussion
Coordination numbers of alkali atoms
Fig.1a,b show that in the first approximation the distributions of R(M-O) at M=Li or Na are bimodal, with maxima at R1� 2.0 and R2� 3.5µ or R1� 2.4 and R2� 3.8µ, respectively, and clearly expressed minima at Rmin� 2.7 or Rmin� 3.2µ. The values of Rmin divide each distribution into two parts, first of which (R(M-O)<Rmin) characterises strong M-O bonds of ionic-covalent type, and second (R(M-O)>Rmin) – additional weaker M-O contacts with mainly ionic nature. Note that Rmin values are in good accordance with the upper limits of R(M-O), which are frequently used in practice for determination of CNs of lithium and sodium ions without any reason (see, for example, [10]). Accepting W (M-O) value as a more accurate characteristic of strength of M-O bond, we can get on the basis of W (R) dependence that Wmin� 8 or 5% correspond to R(M-O)� Rmin. Thus, the Wmin indicated were accepted as lower limits of W (M-O) values, at which the corresponding M-O contact should be taken into consideration during the calculation of CNcl of M atoms (i.e. of nl values). In our opinion, the total description of coordination sphere of lithium and sodium atoms also requires the indication of the second component of total CN (n2). This component corresponds to the number of M-O contacts of mainly ionic type and is characterised by 1.5%<W (Li-O)<8% or 1.5%<W (Na-O)<5%.
The results of calculations of VDPs of potassium, rubidium and caesium atoms for 559, 142 and 166 oxygen-containing compounds correspondingly, show that R(M-O) distributions (M=K, Rb or Cs) (Fig.1c-e) are characterised only by one maximum at R1� 2.8, 3.1 or 3.2µ, respectively. Therefore, in contrast to lithium and sodium compounds, the division of M-O contacts at M=K, Rb or Cs into several groups is not reasonable. In this connection, during the determination of CNs of potassium, rubidium and caesium ions the choice of Wmin=1.5% seems to be logical (i.e. in this case total CN is equal to CNcl). We found that R(M-O)=3.8 to 4.1µ corresponds to the Wmin indicated. Thus, R(M-O)� 4.1µ characterises the maximum distances, at which appreciable interatomic interaction can correspond to K-O, Rb-O or Cs-O contacts. Also, it should be noted that monomodal character of R(M-O) distributions at M=K, Rb or Cs may be interpreted as an effect of the mainly ionic nature of all M-O contacts of the same type with W>1.5%, independently of R(M-O) values.
Let us consider two examples of determination of CNs of alkali atoms using above-mentioned principles.
In structure of a -Na2Cr2O7 [10] according to the authors, Na1 and Na2 atoms are characterised by CN=7 with regard to Na-O contacts with R(Na-O)�3.3µ. The authors do not explain the reasons of the choice of upper limit of lengths of Na-O bonds, however, calculations of VDPs (Tables 1,2) show, that at the consideration of all Na-O contacts with R(Na-O)<Rmin classical coordination numbers of sodium atoms are in agreement with CN, specified in the primary source. For the calculation of total CN of Na1 and Na2 atoms, also it is necessary to consider weaker Na-O contacts with W >1.5%, in view of which total CN should be written as 7+1 and 7+2, respectively. Fig.2a,b show that O3, O6 and O7 atoms, Na-O contacts with participation of which determine n2 values and were not considered in [10], give the appreciable contribution to the formation of atomic domains of sodium (on Fig.2 corresponding faces are shaded).
According to [11], in structure of Rb1.67[Pt(C2O4)2]Ç1.5H2O crystallographically independent Rb1, Rb2, Rb3, Rb4 and Rb5 atoms have CN=7, 8, 8, 7 and 7, respectively, at that the Rb-O contacts with R(Rb-O)�3.3µ were only in consideration. The established characteristics of VDPs (tables 3-7) show, that for the given atoms also it is necessary to take into account Rb-O contacts with R(Rb-O)=3.3 to 4.1µ and W>1.5%. Thus, on our data CNs of all Rb atoms differ from those specified in the primary source and equal 9, 10, 10, 9 and 11, respectively. Note that contacts, which are not only characterised by W <1.5%, but also are ‘indirect’, correspond to almost all Rb and Cs atoms, which take part in formation of domains of Rb2-5 atoms (tables 4-7), excepting Rb2 in the VDP of Rb2 atom. The data of tables 1-7 confirm conclusions of [9], indicating that all ‘indirect’ contacts (including Rb-O contacts) should not be considered as chemical bonds in view of the condition W<1.5%.
Effect of constancy of volume of atomic domains
The results of calculation of the characteristics of VDPs for 2749 crystallographic sorts of M atoms in structure of compounds, data on which are contained in the above-mentioned database, and CNs of M atoms defined as CNcl using the method described are given in tables 8-12. As can be seen from tables 8-12, at CNcl� 6 the hypothesis of constancy of volume of atomic domains (estimated by the volume of their VDPs (VVDP)) for M atoms seems to be true overall. Some deviations of VVDP from mean values (in particular, for Na atoms at CNcl=9 and for K and Rb atoms at CNcl=18) are not numerous. They occur because corresponding CNcl are typical for the atoms in structure of thermodynamically metastable (under standard conditions) compounds (table 13). Features of a structure of the corresponding compounds also explain non-monotonic change of VVDP for lithium atoms. In particular, among 14 compounds, in which lithium atoms are characterised by CNcl=8, in 13 structures they are coordinated by the molecules of crown-ether and thus, the dimension of their atomic domains is determined by a diameter of ligand cavity. Data on unique compound SrLi2Al4(OH)4(PO4)4 [20], in structure of which lithium atoms have CNcl=7, cannot be sufficient for statistically significant estimation of the dimensions of atomic domains for Li at that CNcl. The unusually low CNcl=3, found in structures of LiBa3A3Ti5O21 (A=Nb, Ta or Sb) [21], is result of that the indicated compounds are intercalation phases.
In our opinion, increased values of VVDP of lithium and sodium ions at small CNcl (4 or 5) are caused by strengthening of the covalent component of M-O bonds (M=Li or Na) during decreasing CN of M atoms and by simultaneous distortion of atomic domains. For detailed estimation of the VDP distortion we use the G3 quantity, which was earlier proposed as a criterion of the uniformity of a multiregular system [4]:
where V[P(pi)] is the volume of the VDP (designated as P(pi)) of a point pi, ri is the distance from a point of P(pi) to the central point (pi), n is space dimensionality (n=3) and Z is the number of basis points in unit cell of multiregular system. In particular, when Z=1 and a point p coincides with the center of gravity of VDP, G3 is equal to the dimensionless second moment of inertia of the VDP. As was shown in [4], G3 of a single VDP is an integral parameter of a degree of VDP distortion. Sphere is characterized by the smallest G3 value (0.07697) therefore, the more G3 value of a VDP the stronger its distortion (the smaller the degree of its sphericity).
Thus, high values of G3 also indicate appreciable directivity of M-O interactions namely at small CNcl. The criterion of nondirectivity of forces of interatomic interaction (G3<0.082 [22]) and the data in table 3 allow one to neglect the covalent component of M-O bonds only at sufficiently large CNcl (8 for M=Li or more than 8 for M=Na) with regard to an error in G3 determination. The similar conclusion can be made for compounds of potassium, rubidium and caesium atoms. However, for K, Rb or Cs atoms CNcl>8 is the most typical (tables 10-12), whereas for lithium and sodium compounds the calculations give a directly opposite result (tables 8,9). This fact also indicates the difference of the nature of M-O contacts in compared groups of compounds.
Application of the model of deformable spheres
The model of deformable spheres [23] may be used for alkali atoms at CNcl� 6. That is proved by indicated constancy of VVDP and by isotropic character of distortion of their atomic domains, since the value of shift of M atom from a centre of gravity of VDP (DA) is practically equal to zero for all CNcl (tables 8-12). The degree of deformation of an atomic domain decreases with increase of the size of atom M, that is confirmed not only by the analysis of G3 values, but also by the character of change of radii (Rsd) of spherical domains, volume of which is equal to VVDP, in comparison with the values of radii [7] of corresponding ions (Fig.3). Note that, within the framework of the model of deformable spheres, Rsd can be considered as a value being proportional to the radius of an atom or an ion in the given electron state before placing it in a crystal field. For lithium and sodium atoms the significant deformation of their domains caused by formation of ionic-covalent bonds leads to appreciable increase of Rsd in comparison with ionic radii given in [7]. For K, Rb and Cs atoms the differences among Rsd and corresponding ionic radii do not exceed 0.05µ (Fig.3), that, in our opinion, also confirms nondirectivity of M-O interactions (M=K, Rb or Cs).
References
[1] Pearson, W.: The crystal chemistry and physics of metals and alloys. Wiley-Interscience 1972.
[2] Wiberg, K.B., Bader, R.F.W., Lau, C.D.H.: Theoretical analysis of hydrocarbon properties. 2. Additivity of group properties and the origin of strain energy. J. Am. Chem. Soc. 209 (1987) 1001-1012.
[3] Tsirelson, V.G., Zou, P.F., Tang, T.H., Bader, R.F.W.: Topological definition of crystal structure: determination of the bonded interactions in solid molecular chlorine. Acta Cryst. A51 (1995) 143-153.
[4] Blatov, V.A., Shevchenko, A.P., Serezhkin, V.N.: Crystal space analysis by means of Voronoi-Dirichlet polyhedra. Acta Cryst. A51 (1995) 909-916.
[5] Blatov, V.A., Shevchenko, A.P., Serezhkin, V.N.: Atomic domains of uranium(II-VI) in oxygen-containing compounds. Dokl. Acad. Nauk 343 (1995) 771-774.
[6] Serezhkin, V.N., Blatov, V.A., Kuklina, E.S.: Voronoi-Dirichlet polyhedra of Zr(IV) atoms in fluorine-containing compounds. Koord. Khim. 22 (1996) 645-647.
[7] Shannon, R.D.: Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A32 (1976) 751-767.
[8] Frank, F.C., Kasper, J.C.: Complex alloy structures regarded as sphere packing Acta Cryst. 11 (1958) 184-190.
[9] O'Keeffe, M.: A proposed rigorous definition of coordination number. Acta Cryst. A35 (1979) 772-775.
[10] Panagiotopoulos, N.Ch., Brown, I.D.: The crystal structure of
a -Na2Cr2O7 and the a –b phase transition. Acta Cryst. B29 (1973) 890-894.[11] Kobajashi, A., Sasaki, Y., Kobajashi, H.: Structural studies of commensurate peierls state of Rb1.67[Pt(C2O4)2]
Ç 1.5H2O. Bull. Chem. Soc. Jpn. 52 (1979) 3682-3691.[12] Prewitt, C.T., Sueno, S., Papike, J.J.: The crystal structures of high albite and monalbite at high temperatures. Am. Miner. 61 (1976) 1213-1225.
[13] Winter, J.K., Okamura, F.P., Ghose, S.: A high temperature structural study of high albite, monalbite, and the analbite-monalbite phase transition. Am. Miner. 64 (1979) 409-423.
[14] Felsche, J.: The alkali problem in the crystal structure of beta alumina. Z. Kristallogr. 127 (1968) 94-100.
[15] Le Flem, G., Salmon, R.: Sur de nouvelles phases oxygene es de type pyrochlore lacunaire. Compt. Rend. Ser. C. 27 (1970) 1182-1184.
[16] Michel, C., Guyomarch, A., Raveau, B.: Nouveaux echangeurs cationiques avec une structure a tunnels entrecroises: les oxides A12M33O90 et A12M33O90(H2O)12. J. Solid State Chem. 22 (1977) 393-403.
[17] Darriet, B., Rat, M., Galy, J., Hagenmueller, P.: Sur quelques nouveaux pyrochlores des systemes MTO3–WO3 et MTO3–TeO3 (M=K, Rb, Cs, Tl; T=Nb, Ta). Mater. Res. Bull. 6 (1971) 1305-1316.
[18] Bydanov, N. N., Chernaya, T. S., Muradyan, L. A., Sarin, V. A., Rider, E. E., Yanovskii, V. K., Bosenko, A. A.: Neutron-diffraction refinement of atomic structures of crystals of RbNbWO6 and TlNbWO6. Kristallografiya. 32 (1987) 363-368.
[19] Driouiche, A., Abraham, F., Touboul, M., Figlarz, M.: Rb1.1W1.65O5.5. Synthesis and characterization of cubic pyrochlore-type rubidium and caesium tungstates with a lacunar host lattice. Mater. Res. Bull. 26 (1991) 901-908.
[20] Moore, P.B., Araki, T.: Palermoite, SrLi2(Al4(OH)4(PO4)4). Its atomic arrangement and relationship to carmitnite, Pb2(Fe4(OH)4(AsO4)4). Am. Miner. 60 (1975) 460-465.
[21] Mercey, C., Groult, D., Raveau, B.: Insertion du lithium dans les oxydes de type A3M8O21: les composes LiBaM3Ti5O21. Mater. Res. Bull. 13 (1978) 797-804.
[22] Blatov, V.A., Pol’kin, V.A., Serezhkin, V.N.: Polymorphism of elementary substances and the principle of uniformity. Crystallogr. Rep. 39 (1994) 402-408.
[23] Blatov, V.A., Serezhkin, V.N.: Order and topology in systems with many particles. Acta Cryst. A53 (1997) 144-160.
Table 1. Results of calculation of VDP of Na(1) atom in structure of
a -Na2Cr2O7*Central atom: Na(1) (x=0.338; y=0.343; z=0.726)
VDP volume = 15.927µ3, surface area = 36.222µ2,
Rsd=1.561µ, G3=0.08282, DA=0.072µ
Atom L |
x |
y |
z |
R(Na-L), µ |
W , % |
O(3) |
0.154 | 0.411 | 0.509 | 2.368 | 17.43 |
O(4) |
0.334 | 0.154 | 0.576 | 2.422 | 16.79 |
O(2) |
0.235 | 0.146 | 0.884 | 2.561 | 13.35 |
O(4) |
0.666 | 0.346 | 0.924 | 2.601 | 13.61 |
O(1) |
0.643 | 0.544 | 0.678 | 2.654 | 12.31 |
O(5) |
0.411 | 0.613 | 0.837 | 2.761 | 10.49 |
O(6) |
0.152 | 0.402 | 0.911 | 2.835 | 10.43 |
O(6) |
-0.152 | 0.098 | 0.589 | 3.423 | 4.94 ## |
#O(2) |
0.765 | 0.354 | 0.616 | 3.797 | 0.13 ## |
#O(5) |
0.589 | 0.387 | 1.163 | 3.889 | 0.53 ## |
*The radius of sphere, volume of which is equal to volume of VDP (Rsd), the characteristic of sphericity (G3) and the shift of sodium atom from a centre of gravity of VDP (DA) are specified as the general parameters of VDP, besides its volume and surface area. In each line of the table the name of L atom, its coordinates (x, y, z), interatomic distance (R(Na-L)) and solid angle (
W ), at which corresponding face of VDP is ‘visible’ from a point, coinciding with sodium atom (or L) are consequently given. The symbol ‘#’ marks atoms, which are ‘indirect’ neighbours according to criterion [12]. W values corresponding to atoms, which were not taken into account by the authors [13] during determination of CN of sodium atoms, are marked by '##'.
Table 2. Results of calculation of VDP of Na(2) atom in structure of
a -Na2Cr2O7*Central atom: Na(2) (x=0.765; y=0.238; z=0.393)
VDP volume = 15.605µ3, surface area = 35.525µ2,
Rsd=1.550µ, G3=0.08263, DA=0.094µ
Atom L |
x |
y |
z |
R(Na-L), µ |
W , % |
O(5) |
0.411 | 0.113 | 0.337 | 2.403 | 15.74 |
O(6) |
0.848 | 0.098 | 0.589 | 2.426 | 16.06 |
O(2) |
0.765 | 0.354 | 0.616 | 2.448 | 14.98 |
O(1) |
0.643 | 0.044 | 0.178 | 2.526 | 14.33 |
O(3) |
1.154 | 0.411 | 0.509 | 2.658 | 12.37 |
O(7) |
0.950 | 0.386 | 0.209 | 2.737 | 10.40 |
O(5) |
0.589 | 0.387 | 0.163 | 2.939 | 9.52 |
O(7) |
1.050 | 0.114 | 0.291 | 3.376 | 3.82 ## |
O(3) |
0.846 | 0.589 | 0.491 | 3.507 | 2.77 ## |
#O(4) |
0.666 | -0.154 | 0.424 | 3.853 | <0.01 ## |
*See the remark to table 1.
Table 3. Results of calculation of VDP of Rb(1) atom in structure of Rb1.67[Pt(C2O4)2]*
Central atom: Rb(1) (x=0.267; y=0.930; z=0.537)
VDP volume = 25.410µ3, surface area = 48.755µ2,
Rsd=1.824µ, G3=0.08305, DA=0.096µ
Atom L |
x |
y |
z |
R(Rb-L), µ |
W , % |
O(25) |
0.496 |
0.715 |
0.705 |
2.892 |
12.73 |
O(19) |
0.051 |
1.108 |
0.667 |
2.902 |
14.39 |
O(8) |
0.615 |
0.811 |
0.624 |
2.958 |
12.53 |
O(20) |
0.283 |
0.756 |
0.378 |
3.070 |
13.21 |
O(15) |
0.276 |
1.058 |
0.386 |
3.140 |
13.21 |
O(3) |
-0.104 |
1.106 |
0.321 |
3.161 |
10.70 |
O(7) |
0.486 |
0.928 |
0.815 |
3.175 |
9.27 |
O(1) |
0.044 |
1.003 |
0.195 |
3.499 |
5.24 |
O(3) |
0.104 |
0.894 |
0.679 |
3.512 |
6.87 |
O(19) |
-0.051 |
0.892 |
0.333 |
4.164 |
0.89 ## |
#O(27) |
0.143 |
1.228 |
0.702 |
4.338 |
0.79 ## |
#O(16) |
-0.071 |
1.284 |
0.325 |
4.523 |
0.17 ## |
#O(4) |
0.401 |
0.776 |
0.919 |
4.544 |
0.01 ## |
*See the remark to table 1.
Table 4. Results of calculation of VDP of Rb(2) atom in structure of Rb1.67[Pt(C2O4)2]*
Central atom: Rb(2) (x=0.462; y=0.401; z=0.873)
VDP volume = 24.848µ3, surface area = 47.490µ2,
Rsd=1.810µ, G3=0.08219, DA=0.041µ
Atom L |
x |
y |
z |
R(Rb-L), µ |
W , % |
O(24) |
0.233 |
0.380 |
0.764 |
2.892 |
15.03 |
O(26) |
0.374 |
0.436 |
0.593 |
2.921 |
14.28 |
O(12) |
0.522 |
0.537 |
0.844 |
3.038 |
12.94 |
O(10) |
0.218 |
0.563 |
1.006 |
3.053 |
10.77 |
O(4) |
0.599 |
0.224 |
1.081 |
3.103 |
8.59 |
O(18) |
0.793 |
0.245 |
0.837 |
3.116 |
9.98 |
O(12) |
0.478 |
0.463 |
1.156 |
3.140 |
9.02 |
O(2) |
0.763 |
0.123 |
0.972 |
3.271 |
7.52 |
#C(2) |
0.737 |
0.154 |
1.085 |
3.406 |
0.88 ## |
O(14) |
0.874 |
0.247 |
1.120 |
3.583 |
5.27 |
#C(6) |
0.672 |
0.474 |
0.878 |
3.652 |
0.15 ## |
#O(22) |
0.189 |
0.396 |
0.943 |
3.921 |
0.23 ## |
O(16) |
0.071 |
0.716 |
0.675 |
3.946 |
4.20 |
O(14) |
0.126 |
0.753 |
0.880 |
4.162 |
1.10 ## |
Rb(2) |
0.538 |
0.599 |
1.127 |
4.363 |
0.03 ## |
*See the remark to table 1.
Table 5. Results of calculation of VDP of Rb(3) atom in structure of Rb1.67[Pt(C2O4)2]*
Central atom: Rb(3) (x=0.713; y=0.336; z=0.424)
VDP volume = 22.776µ3, surface area = 44.303µ2,
Rsd=1.758µ, G3=0.08126, DA=0.130µ
Atom L |
x |
y |
z |
R(Rb-L), µ |
W , % |
O(16) |
0.929 |
0.284 |
0.325 |
2.862 |
14.31 |
O(12) |
0.478 |
0.463 |
0.156 |
2.916 |
11.50 |
O(20) |
0.717 |
0.244 |
0.622 |
2.955 |
11.21 |
O(11) |
0.346 |
0.542 |
0.345 |
2.981 |
10.06 |
O(11) |
0.654 |
0.458 |
0.655 |
2.993 |
11.60 |
O(3) |
0.896 |
0.106 |
0.321 |
3.066 |
11.13 |
O(25) |
0.504 |
0.285 |
0.295 |
3.072 |
9.50 |
O(26) |
0.626 |
0.564 |
0.407 |
3.225 |
9.32 |
O(19) |
1.051 |
0.108 |
0.667 |
3.381 |
7.60 |
#C(10) |
0.823 |
0.213 |
0.732 |
3.644 |
0.03 ## |
O(27) |
1.143 |
0.228 |
0.702 |
4.041 |
3.37 |
#O(9) |
0.899 |
0.351 |
0.813 |
4.088 |
0.21 ## |
O(4) |
0.599 |
0.224 |
0.081 |
4.129 |
0.18 ## |
*See the remark to table 1.
Table 6. Results of calculation of VDP of Rb(4) atom in structure of Rb1.67[Pt(C2O4)2]*
Central atom: Rb(4) (x=0.865; y=0.678; z=0.501)
VDP volume = 27.864µ3, surface area = 51.966µ2,
Rsd=1.880µ, G3=0.08682, DA=0.165µ
Atom L |
x |
y |
z |
R(Rb-L), µ |
W , % |
O(16) |
1.071 |
0.716 |
0.675 |
2.946 |
13.92 |
O(24) |
0.767 |
0.620 |
0.236 |
2.994 |
13.68 |
O(27) |
0.857 |
0.772 |
0.298 |
3.000 |
13.68 |
O(23) |
0.884 |
0.522 |
0.615 |
3.014 |
13.16 |
O(8) |
0.615 |
0.811 |
0.624 |
3.027 |
12.72 |
O(23) |
1.116 |
0.478 |
0.385 |
3.087 |
11.47 |
O(6) |
0.868 |
0.713 |
0.789 |
3.191 |
7.37 |
O(15) |
0.724 |
0.942 |
0.614 |
3.605 |
6.00 |
#C(8) |
1.014 |
0.782 |
0.757 |
3.631 |
0.01 ## |
#C(11) |
0.950 |
0.506 |
0.738 |
3.653 |
0.20 ## |
#C(7) |
0.838 |
0.888 |
0.727 |
3.831 |
0.18 ## |
O(24) |
1.233 |
0.380 |
0.764 |
4.090 |
2.96 |
#O(26) |
1.374 |
0.436 |
0.593 |
4.152 |
1.46 ## |
#O(26) |
0.626 |
0.564 |
0.407 |
4.368 |
0.80 ## |
#Rb(5) |
0.513 |
0.883 |
0.088 |
4.537 |
1.17 ## |
#O(15) |
0.276 |
1.058 |
0.386 |
4.967 |
1.23 ## |
*See the remark to table 1.
Table 7. Results of calculation of VDP of Rb(5) atom in structure of Rb1.67[Pt(C2O4)2]*
Central atom: Rb(5) (x=0.513; y=0.883; z=0.088)
VDP volume = 26.881µ3, surface area = 49.498µ2,
Rsd=1.858µ, G3=0.08449, DA=0.218µ
Atom L |
x |
y |
z |
R(Rb-L), µ |
W , % |
O(4) |
0.401 |
0.776 |
-0.081 |
3.002 |
10.72 |
O(27) |
0.857 |
0.772 |
0.298 |
3.062 |
12.42 |
O(5) |
0.747 |
0.808 |
-0.031 |
3.080 |
9.17 |
O(7) |
0.486 |
0.928 |
-0.185 |
3.168 |
9.07 |
O(13) |
0.206 |
1.071 |
0.169 |
3.174 |
11.67 |
O(7) |
0.514 |
1.072 |
0.185 |
3.209 |
10.38 |
O(17) |
0.124 |
1.078 |
-0.117 |
3.247 |
8.13 |
O(24) |
0.767 |
0.620 |
0.236 |
3.310 |
9.07 |
O(2) |
0.237 |
0.877 |
0.028 |
3.357 |
6.03 |
#C(2) |
0.263 |
0.846 |
-0.085 |
3.370 |
0.75 ## |
#C(3) |
0.632 |
0.849 |
-0.149 |
3.381 |
0.60 ## |
O(22) |
0.811 |
0.604 |
0.057 |
3.388 |
5.37 |
#C(3) |
0.368 |
1.151 |
0.149 |
3.525 |
1.29 ## |
#C(12) |
0.863 |
0.580 |
0.183 |
3.556 |
0.58 ## |
O(5) |
0.253 |
1.192 |
0.031 |
3.688 |
2.74 |
#Rb(4) |
0.865 |
0.678 |
0.501 |
4.537 |
1.17 ## |
#O(15) |
0.276 |
1.058 |
0.386 |
4.567 |
0.84 ## |
*See the remark to table 1.
Table 8. The characteristics of VDP of lithium atoms depending on their CN
CN of Li atoms |
The number of com-pounds |
The number of Li atoms |
VVDP, µ3* |
SVDP, µ2* |
Rsd, µ* |
G3, � 103* |
DA, µ** |
3 |
3 |
3 |
10.3(9) |
27(1) |
1.35(4) |
83.2(3) |
0.00(1) |
4 |
96 |
131 |
11.8(1) |
32.8(4) |
1.41(1) |
94.0(7) |
0.08(7) |
5 |
35 |
37 |
11.8(3) |
31.3(5) |
1.41(1) |
91(1) |
0.13(8) |
6 |
116 |
142 |
10.3(2) |
28.1(3) |
1.35(1) |
84.6(3) |
0.04(4) |
7 |
1 |
1 |
12.1 |
30.3 |
1.42 |
86.5 |
0.13 |
8 |
14 |
17 |
11.1(1) |
28.2(2) |
1.38(1) |
81.4(3) |
0.03(2) |
4 ñ8*** |
252 |
328 |
11.1(1) |
30.3(3) |
1.38(1) |
89.1(6) |
0.06(7) |
*The values of fiducial intervals, which correspond to 95% of fiducial probability are given in brackets.
**The values of standard deviations are given in brackets, since the distributions of DA values deviate from normal distribution for all CNs.
***The data for all crystallographic sorts of lithium atoms are included in this line irrespectively of their CNs.
Table 9. The characteristics of VDP of sodium atoms depending on their CN*
CN of Na atoms |
The number of com-pounds |
The number of Na atoms |
VVDP, µ3* |
SVDP, µ2* |
Rsd, µ* |
G3, � 103* |
DA, µ* |
4 |
8 |
8 |
20(1) |
43(2) |
1.69(4) |
87(1) |
0(0) |
5 |
10 |
10 |
16.6(9) |
39(2) |
1.58(3) |
89(2) |
0.11(8) |
6 |
343 |
520 |
15.0(1) |
35.9(2) |
1.53(1) |
85.3(2) |
0.07(6) |
7 |
139 |
171 |
15.3(2) |
35.5(3) |
1.54(1) |
84.6(3) |
0.09(5) |
8 |
179 |
200 |
15.1(2) |
34.4(3) |
1.53(1) |
82.9(3) |
0.06(5) |
9 |
32 |
36 |
16.8(8) |
37(1) |
1.58(2) |
82.6(7) |
0.06(4) |
10 |
10 |
10 |
16(1) |
35(2) |
1.56(4) |
81(1) |
0.04(3) |
12 |
18 |
19 |
15.5(8) |
33(1) |
1.54(3) |
79(1) |
0.02(3) |
4 ñ12* |
620 |
974 |
15.2(1) |
35.6(1) |
1.54(1) |
84.5(1) |
0.06(6) |
*See the remarks to table 8.
Table 10. The characteristics of VDP of potassium atoms depending on their CN*
CN of K atoms |
The number of com-pounds |
The number of K atoms |
VVDP, µ3* |
SVDP, µ2* |
Rsd, µ |
G3, � 103 |
DA, µ* |
6 |
9 |
11 |
19(2) |
42(3) |
1.66(6) |
83.6(8) |
0.02(4) |
7 |
16 |
16 |
22(1) |
45(2) |
1.73(4) |
85(2) |
0.1(1) |
8 |
103 |
111 |
20.6(3) |
42.7(5) |
1.699(9) |
83.4(6) |
0.08(7) |
9 |
127 |
150 |
20.5(2) |
42.0(3) |
1.698(5) |
82.4(2) |
0.08(6) |
10 |
193 |
228 |
20.5(2) |
41.6(3) |
1.697(5) |
81.9(3) |
0.07(6) |
11 |
107 |
124 |
21.1(2) |
42.0(4) |
1.713(7) |
81.5(3) |
0.08(5) |
12 |
162 |
179 |
21.0(3) |
41.2(4) |
1.708(7) |
80.6(3) |
0.04(6) |
13 |
34 |
37 |
21.2(7) |
42(1) |
1.72(2) |
81.1(3) |
0.07(5) |
14 |
23 |
25 |
21.8(7) |
42(1) |
1.73(2) |
80.5(4) |
0.06(6) |
15 |
11 |
13 |
21(1) |
41(2) |
1.72(3) |
80(1) |
0.04(7) |
16 |
2 |
2 |
23(1) |
42.9(9) |
1.75(3) |
81(3) |
0.06(5) |
6 ñ16** |
560 |
930 |
20.8(1) |
41.8(2) |
1.704(3) |
81.9(1) |
0.07(6) |
18 |
1 |
1 |
27.4 |
47.7 |
1.86 |
79.7 |
0.00 |
*See the remarks to table 8.
Table 11. The characteristics of VDP of rubidium atoms depending on their CN*
CN of Rb atoms |
The number of compounds |
The number of Rb atoms |
VVDP, µ3* |
SVDP, µ2* |
Rsd, µ |
G3, � 103 |
DA, µ* |
8 |
12 |
12 |
23(2) |
46(3) |
1.77(5) |
82.1(9) |
0.03(5) |
9 |
32 |
37 |
24.0(5) |
46.4(9) |
1.79(1) |
82.3(7) |
0.09(5) |
10 |
58 |
69 |
23.2(4) |
45.0(6) |
1.77(1) |
82.1(3) |
0.1(1) |
11 |
34 |
38 |
23.6(5) |
45.3(8) |
1.78(1) |
81.2(4) |
0.07(5) |
12 |
57 |
68 |
23.2(4) |
44.2(6) |
1.77(1) |
80.6(3) |
0.05(5) |
13 |
10 |
11 |
24.3(6) |
46(1) |
1.80(2) |
82(1) |
0.09(5) |
14 |
13 |
13 |
23.0(8) |
43(1) |
1.76(2) |
80(1) |
0.05(6) |
15 |
3 |
4 |
25(2) |
45(2) |
1.81(3) |
79.7(4) |
0.07(2) |
16 |
2 |
2 |
24(2) |
45(4) |
1.80(4) |
80.6(3) |
0.1(1) |
8 ñ16** |
180 |
254 |
23.4(2) |
44.9(3) |
1.775(5) |
81.1(2) |
0.07(9) |
18 |
4 |
4 |
29(2) |
50(2) |
1.90(3) |
80(1) |
0.0(1) |
*See the remarks to table 8.
Table 12. The characteristics of VDP of caesium atoms depending on their CN*
CN of Cs atoms |
The number of com-pounds |
The number of Cs atoms |
VVDP, µ3* |
SVDP, µ2* |
Rsd, µ* |
G3, � 103* |
DA, µ** |
6 |
1 |
1 |
31.2 |
57.8 |
1.96 |
84.1 |
0.00 |
8 |
6 |
6 |
29(4) |
53(5) |
1.90(8) |
83(2) |
0.06(5) |
9 |
9 |
9 |
27(1) |
49(2) |
1.85(3) |
81.1(8) |
0.06(5) |
10 |
26 |
31 |
28.0(6) |
51.0(7) |
1.88(2) |
81.6(4) |
0.07(4) |
11 |
30 |
35 |
28.2(5) |
50.8(7) |
1.89(1) |
81.3(5) |
0.08(5) |
12 |
59 |
73 |
27.5(4) |
49.4(6) |
1.87(1) |
80.6(3) |
0.06(6) |
13 |
26 |
32 |
28.0(6) |
49.8(8) |
1.88(1) |
81.1(5) |
0.09(6) |
14 |
27 |
30 |
26.6(5) |
47.8(7) |
1.85(1) |
80.3(4) |
0.05(4) |
15 |
14 |
15 |
28(1) |
49(1) |
1.87(2) |
80.1(5) |
0.06(3) |
16 |
3 |
3 |
28(5) |
49(5) |
1.9(1) |
79.6(5) |
0.09(6) |
17 |
1 |
1 |
27.2 |
47.9 |
1.87 |
80.1 |
0.06 |
18 |
14 |
18 |
28.6(5) |
49.1(6) |
1.90(1) |
79.9(4) |
0.04(5) |
20 |
1 |
1 |
29.2 |
49.8 |
1.91 |
80.1 |
0.06 |
6 ñ 20*** |
166 |
255 |
27.7(2) |
49.7(3) |
1.88(1) |
80.8(2) |
0.07(5) |
*See the remarks to table 8.
Table 13. The compounds, in structures of which alkali atoms with abnormally high VVDP values were found
Compound |
M atoms |
CNcl |
VVDP, µ3 |
Remarks |
References |
NaAlSi3O8 |
Na(1) |
9 |
17.9 ñ18.9* |
The compounds have been obtained at T>600 �C |
[12,13] |
Na2Al22O34 |
Na(1) |
9 |
23.8 |
Superionic conductor of b -Al2O3 type |
[14] |
KCr0.33W1.6O6 |
K(1) |
18 |
27.4 |
Defective structure of pyrochlore |
[15] |
Rb12Nb30W3O90 |
Rb(1) |
18 |
30.5 |
Tunnel structure |
[16] |
RbNbTeO6 |
Rb(1) |
18 |
28.8 |
Defective structure of pyrochlore |
[17] |
RbNbWO6 |
Rb(1) |
18 |
28.7 |
- “ - |
[18] |
RbW1.6O6 |
Rb(1) |
18 |
26.6 |
- “ - |
[19] |
*Depending on temperature of experiment.
a
b
c
d
e
Fig.1. R(M-O) distributions in oxygen-containing compounds of
a) lithium (3093 Li-O contacts); b) sodium (10081 Na-O contacts); c) potassium (11323 K-O contacts);
d) rubidium (2793 Rb-O contacts); e) caesium (3775 Cs-O contacts).
The values on the axis of ordinates are expressed in percentage of the total number of corresponding M-O contacts.
a
b
Fig.2. VDPs and environment of Na(1) (a) and Na(2) (b) atoms in the structure of a -Na2Cr2O7. The faces of VDPs, corresponding to Na-O contacts with 1.5%<W <5% are shaded.
Fig.3. Dependence of Rsd (—� —) or Rion (—n —) on chemical sort of an alkali atom. The values calculated by averaging ionic radius for all CNs given in [7] are accepted as Rion (µ), namely: 0.90 (Li+); 1.27 (Na+); 1.64 (K+); 1.79 (Rb+); 1.93 (Cs+).