Samara State University, Samara, Russia

Abstract — Structural and topological studies of the coordination environment of Zr(IV) atoms in oxygen-containing crystal compounds are carried out by means of the Voronoi-Dirichlet polyhedrons (VDPs). A rigorous method of determining the combinatorial-topological type of coordination polyhedron (CP) consists of analyzing the appropriate dual VDP. To account for the distortions of the coordination sphere caused by the thermal motion of atoms, dynamical VDPs and CPs are introduced. It is shown that, for high coordination numbers of a zirconium atom (C.N. 6), the volume of ZrO_n VDP is virtually independent of C.N. and equals 9.04(6) µ³. The oxygen-containing sublattices of the compounds studied are found to be topologically similar to the aperiodic systems that model fluids.

An analysis of the VDPs (Table 1) indicates that the C.N. of Zr(IV) atoms in the oxygen environment ranges from 4 to 9, although C.N. 6 and the octahedral CP are most typical for Zr(IV). An increase in the C.N. of zirconium atoms and the respective increase in the number of VDP faces lead to a monotonic decrease in its surface area and in the G₃ value characterizing the degree of uniformity of the zirconium environment [4], thereby indicating that the VDP shape approaches a sphere. As in the previously studied uranium and zirconium coordination compounds, the volume of the VDP of complexing atom with a C.N. 6 virtually does not change and is equal to 9.04(6) µ³ However, the fact that the VDP volume is considerably greater for C.N. 4 and 5 may be due to either one of the following: (1) to a profound difference in the electronic structures of the zirconium complexes having C.N. < 6 and C.N. 6, or (2) to the errors that are introduced by the chosen dividing factor K_d [2] because not only oxygen atoms contribute to the formation of VDP at C.N. 4 or 5. Unfortunately, we failed to determine which one of these was the cause because of the low number of the known zirconium compounds having C.N. 4 or 5 (compounds 1 and 2, respectively).

As was already pointed out in [1-3], the VDPs of atoms A that are chemically bonded to the surrounding atoms X are characterized by the linear relationships between the solid angles (W_i) of the VDP faces corresponding to the A-X contacts and the relevant interatomic distances, i.e.,

W_i(A-X) = A - Br_i(A-X)                                      (1)

lnW_i(A-X) = C - Dr_i(A-X).                                  (2)

lnW_i(Zr–O) = 6.64(5) - 1.85(2) r_i(Zr–O),        (3)

with the coefficient of correlation equal to -0.95 for 752 experimental points. Note that the analogous dependence for the Zr-F contacts in ZrF_n CPs [1] is characterized by nearly the same values of the coefficients Á and D [6.67(5) and -1.95(2), respectively]. In our opinion, this fact is evidence for the similarity of the types of Zr-O(F) interactions in the coordination compounds. Note parenthetically that, although the volume of the VDP of composition ZrX_n, with X = F [1] or O (Table 1), is virtually independent of the C.N. of Zr(IV) for n 6, it significantly increases (by 1 µ³) on passing from ZrF_n to ZrO_n, with a simultaneous increase in R_sd from 1.24(1) to 1.29(1) µ. In spite of the fact that we did not use any atomic radii (for Zr, F, O, and others) in calculating the geometric characteristics of VDPs, the difference obtained R_sd(ZrO_n) - R_sd(ZrF_n) = 0.05 µ is close to the difference in the known radii [6] R(O^2-) – R(F^–) 0.06-0.07 µ.

Table 1. Geometric characteristics of the Voronoi-Dirichlet polyhedrons of a zirconium atom*

In describing the topology of a many-body system, account was taken of its dynamics using the concept of a Delone dynamical system as an ensemble of the Delone static systems (as defined in [9]). The crystal lattice can be regarded as the Delone dynamical system as well, provided that the atomic vibrations are taken into account. The structural-topological properties of the nearest surroundings of the p, atom can be naturally characterized by introducing the dynamical VDPs [P^D(p_i)] into the Delone dynamical system. 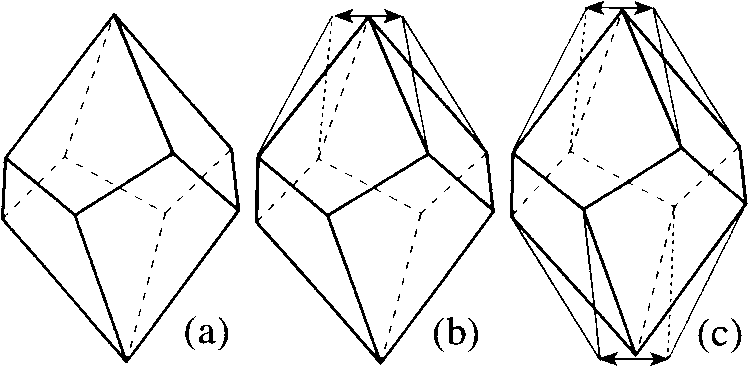P^D(p_i) is defined as a set [P_k(p_i)] of the static VDPs belonging to the ensemble of Delone static systems, with the weight w _k equal for each P_k(p_i) to the probability of realizing P_k(p_i) within the dynamical system. Thus, P^D(p_i) is a VDP averaged over all VDPs that are realized for p_i in the moving system during a certain time interval. Let us call the maximum value of w _k (w _max) the degree of stability of P^D(p_i); P^D(p_i), for which (w _max = 1, the stable dynamical VDP; and denote P_k(p_i) with w _k = w _max by P_max(p_i). Obviously, the stable P^D(p_i) can occur only in the solid state, where the translational motion of atoms is virtually absent, while the power of the {P_k(p_i)} set is limited. Therefore, the atom in the crystal lattice possesses the stable dynamical VDP, provided that the topology of its surroundings (and, hence, topology of CP) does not change in the course of the oscillatory motion.

A dynamical CP [CP^D(p_i)] dual with the dynamical VDP can be introduced in a similar manner. CP^D(p_i) is a set of all CP_k(p_i) dual with the corresponding P_k(p_i) from P^D(p_i). The data of the structural experiment are ordinarily invoked for determining the "average" P_X-ray(p_i) and CP_X-ray(p_i) polyhedrons, which, in general, differ from P_max(p_i) and CP_max(p_i). Let us consider, as an example, the dynamical CP of the zirconium atom in the structure Zr(IO₃)₄ [10]. In this case, P_X-ray(p_i) and CP_X-ray(p_i) are the tetragonal trapezohedron (Fig. 1a) and tetragonal antiprism, respectively. At the same time, it is known that the VDPs having the (n >3)-fold vertices (the so-called "partial" VDPs [11]) are combinatorially unstable to the arbitrary (infinitesimal) distortion of geometry. For this reason, P^D(Zr) must include the polyhedrons that are formed from P_X-ray(Zr) (Fig. 1a) after splitting one (Fig. 1b) or two (Fig. 1c) of its vertices having n = 4. The corresponding CPs relate to the combinatorial-topological types of bicapped trigonal prism and trigonal dodecahedron, respectively, although geometrically can be assigned to the type of a weakly distorted tetragonal antiprism. Since, among the zirconium eight-vertex CPs, only the trigonal dodecahedron is combinatorially stable (it corresponds to the "general", by definition [11], VDP with the vertices all having n = 3), for C.N. 8, this type of CP must be most often realized for CP_X-ray(Zr), as is actually the case (Table 2). The corresponding P^D(Zr) can include the partial VDPs, and, hence, among the trigonal-dodecahedral CPs_X-ray(Zr), CPs can also occur that are geometrically close to the tetragonal antiprism or bicapped trigonal prism. Inasmuch as the general VDPs are dual with the general CPs having exclusively triangular faces, the known CP types can be divided into two groups: combinatorially stable (general) and combinatorially unstable (partial) polyhedrons. For instance, of the CPs considered in [12], the polyhedrons listed in Table 2 refer to the first group. The remaining combinatorial CP types are partial and must occur in the crystal structures much more rarely.

Fig. 1. Transformation of (a) VDP corresponding to the CP in the form of a tetragonal antiprism into the VDP corresponding to the CP in the form of (b) a bicapped trigonal prism and (c) trigonal dodecahedron. Arrows indicate the directions in which the VDP vertices are split. The transformed parts of VDP are indicated by fine lines.

Table 3 presents the results of applying the described procedure in the combinatorial CP analysis of ZrX_n (X = O or F). As a criterion for constricting the VDP r edge, the condition a r <3s 1 was chosen, where a r is the angle at which the edge r is "seen" from the central atom and a is the error in determining the OZrO angles in the structure. The data in Table 3 indicate that 15 combinatorial types exist for ZrX_n (n = 4, 5, 6, 7, 8, or 9) CPs_X-ray(Zr), of which the octahedron, trigonal dodecahedron, and pentagonal bipyramid are most abundant. CPs_X-ray(Zr), as a whole, are combinatorially stable to the distortions caused by the oscillatory motion of atoms, although, in some cases, P^D(Zr) and CP^D(Zr) contain several combinatorial-topological polyhedron types. A typical example is the Zr(SO₄)₂Ç 4H₂O structure [14], in which CPs_X-ray(Zr) is a trigonal dodecahedron, although it becomes geometrically close to the tetragonal antiprism if the oscillatory motion of the atoms is taken into account.

Fig. 2. Frequency (in percent of sample size n) with which the VDP with a given number of faces occurs in the sample containing the VDPs for the zirconium sublattice in the crystal structures of (a) oxygen-containing coordination compounds (n= 112) and (b) coordination compounds with organic ligands (n = 709) [15]. For each of the histograms, one step in abscissa corresponds to changing the number of VDP faces by unity. The columns corresponding to tetradecahedrons are shaded.

Considering that the CPs can be distorted not only by the lattice dynamics and other factors influencing the accuracy of the structural experiment, but also by other causes, primarily by the peculiarities of the electronic structure of complexes, we have studied the combinatorial stability of CP_X-ray(Zr) to more severe distortions than those satisfying condition a r <3s . Table 3 presents the results of analyzing the combinatorial characteristics of the ZrX_n (X = O or F) polyhedrons obtained from CP_X-ray(Zr) after constricting the edges satisfying condition a r <a _lim (a _lim = 5, 10, 15, 20, or 30). An analysis of the data indicates that the CPs that are typical for C.N. 6 or 7 are topologically fairly stable up to a r = 30 (i.e., their number in the sample either remains unchanged or increases by virtue of the appropriate transformations of the CPs of other combinatorial types), whereas part of the trigonal-dodecahedron-shaped CPs transforms into the bicapped trigonal prisms or tetragonal antiprisms even at a r < 1. Note that the ZrF₉ CPs in the form of a tricapped trigonal prism are low-stable and disappear from the sample at a r > 10 (Table 3). This fact is consistent with the classical idea that the C.N. of zirconium atoms in fluoro-containing compounds does not exceed 8. It is also consistent with the conclusion [1] that the small faces corresponding to the nonvalence Zr–F interactions are present in all ZrF₉ CPs.

Table 2. General combinatorial-topological types of coordination polyhedrons

Fig. 3. Frequency (in percent of sample size n) with which the VDP with a given number (f) of faces occurs in the sample (n = 723, solid line) containing the VDPs for the oxygen sublattice in the crystal structures of oxygen-containing zirconium coordination compounds, and sample (n = 10000, dashed line) containing the VDPs for the points of the ideal-gas system [16].

Table 3. Combinatorial-topological analysis of the Voronoi-Dirichlet and coordination polyhedrons of zirconium

*** The number of the sampled VDPs and CPs of a given type, as obtained after constricting all those VDP edges that correspond to the angle a_r smaller than the indicated limiting value.

Table 4. VDP distribution among the combinatorial-topological types for the zirconium sublattices*