Samara State University, Samara, Russia

Abstract - Some features of the U(II-V) environment in oxygen-containing compounds are studied using the Voronoi-Dirichlet polyhedra (VDPs). The VDP volume of uranium atoms appears to be independent of the coordination number at a fixed oxidation state, and it regularly increases with a decrease in the oxidation state. The method of estimating the oxidation state of the uranium atoms in a crystal structure on the basis of geometric parameters of the VDPs is suggested. The advantages of applying the VDPs to determination of the coordination numbers of atoms in a crystal lattice are demonstrated by a number of examples.

Table 1. Variation in the VDP volume (V_VDP), VDP surface area (S_VDP), radius of spherical domain (R_SD) and volume of the coordination polyhedron (V_CP) of uranium atoms with changing oxidation state (x ) and polyhedron composition

* In the presence of additional U-X_i contacts, the composition of the UO_nX_m polyhedra is written as UO_n+m (if X = O) or UO_n (if X O).

Table 2. VDPs of the uranium atoms in some compounds as calculated by the DIRICHLET program*

*The coordinates of the central atoms (U) of the VDPs and of the atoms that share faces with these VDPs (X_i), as well as some other characteristics, which are not used in this work, are omitted for simplicity. The area of the VDP face that is shared by a pair of the U and X_i atoms and the solid angle corresponding to this face (W _i) are expressed, for convenience, in percents of the total surface area of the uranium VDP (S_VDP) and of the total solid angle of 4p sr, respectively. The notations of all atoms are as in [7,8].

Our results indicate that the number of faces in the VDP of uranium atoms in the sampled structures changes from 6 to 12, depending on the oxidation state (x) of uranium atoms and on the composition and structure of a compound. This variation in the number of faces corresponds to the change in composition of the coordination polyhedron from UO₆ to UO₁₂ (Table 1). Note that, for 14 of 62 sorts of uranium atoms, the CN_VDP exceeds the value reported in the original work (CN_CLASS). A detailed analysis shows that the increase in CN_VDP, compared to CN_CLASS, is due to the presence of additional U-X_i contacts (from I to 6), which were not included in the traditional CN determination because these contacts were abnormally long from the classical point of view (>3 µ). In the structures under consideration, the role of the "additional neighbors" most often belongs to the nonmetal atoms (O or C), although, in two compounds (NaUO₃ and Ba_0.98UO₃), the metal atoms (Na and Ba, respectively) were also found to be the additional neighbors.

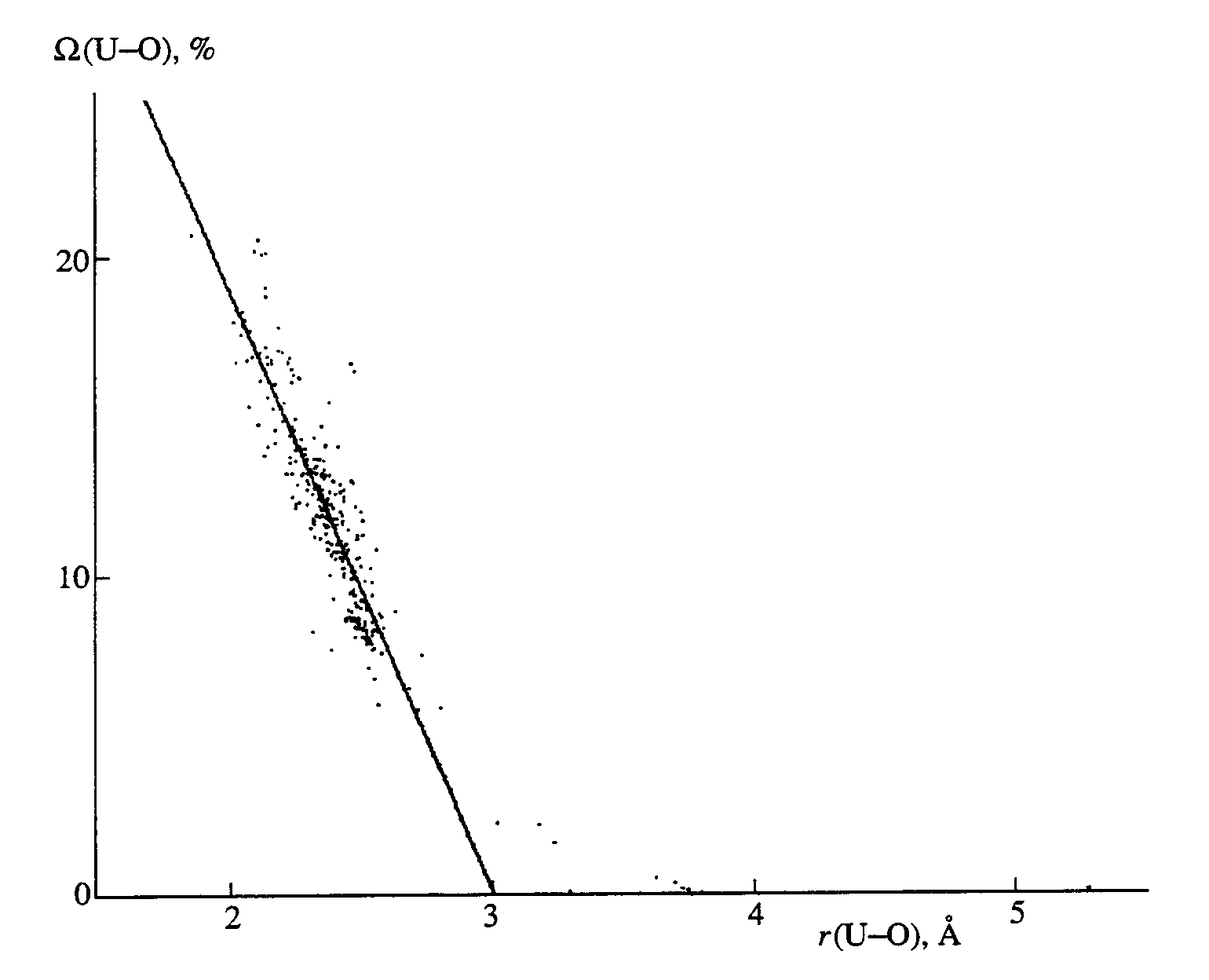
Analysis of the VDPs of the uranium atoms with CN_VDP > CN_CLASS indicates that the additional neighbors X_i correspond to the faces whose summarized area (S_i) does not exceed 3% of the total surface of VDP (S_VDP), and corresponding solid angles (W_i) do not exceed 2.5% of the total solid angle 4p sr. As an example. Table 2 lists the parameters of the uranium VDPs in crystals U₂(CF₃COO)₈ Ç H₂O Ç C₁₈H₃₆N₂O₆ and Ba_0.98UO₃, whose structures were reported in [7, 8], respectively. Note that, for every face of the VDP of atom A, there is a solid angle W_i that is formed by the pyramid with atom A as an apex and face S_i, as a base and is numerically equal to the area of the segment of a unit-radius sphere (centered at atom A) [3, 4]. In terms of our approach, we postulate that the bonding capacity of atom A is distributed over the A-X_i bonds with interatomic distances R_i, proportionally to the values of the solid angles W_i. If one assumes that W_i value for that face of the VDP of atom A that corresponds to the A-X_i contact is proportional to the fraction of the valence electrons of A that are involved in the formation of the A-X_i bond, then the additional interatomic U-X_i contacts for which W_i < 0.17 p sr and S_i < 3% S_VDP can be considered, according to [4], as nonbonded interactions.

The distinction between the bonded and nonbonded U-O_i contacts is clearly demonstrated by the plots of solid angles W _i [or lnW _i(U-O)] versus corresponding interatomic r_i(U-O) distances. For the U(II-V) compounds, the relationship between W _i and r_i(U-O) (the figure) is described, according to linear regression analysis, by equation

W _i (U-O) = 57(1) - 18.8(4)r_i(U-O), (1)

with the correlation coefficient p = -0.89 for 512 VDP faces with W _i > 1%. The remaining VDP faces with W _i l% were ignored when deriving equation (1).

Dependence of the solid angles [W _i(U-O), in percentages of the total solid angle 4p sr] on r(U-O) in 62 Voronoi-Dirichlet polyhedra of the U(II-V) atoms.

The lower limiting value for the considered W_i quantities was taken to be equal to the triple maximum error of solid angle determination s_max(W), which is caused by the errors of X-ray structural experiment. For the sampled compounds, s_max(W) was ca. 0.3%. Note that, for the same 512 experimental points, the relationship between W_i and r_i(U-O) can also be described, according to the least-squares method, by logarithmic dependence with r = -0.90:

lnW_i (U-O) = 6.65(9) - 1.77(4)r_i(U-O). (2)

In equations (1) and (2), the W _i(U-O) values are given in percentages of the total solid angle of the uranium atom, and r_i(U-O) values are given in angstroms.

Table 3. Characteristics of the VDPs of the uranium atoms in different oxidation states*

*For x (U) = VI, the data are taken from [4].

In our opinion, our data (Tables 1 and 3) allow one to conclude that, similarly to the U(VI) compounds, the VDP volume of the uranium atom with the fixed oxidation state (IV or V) and with the coordination polyhedron UO_n (6 n 12) is independent, to within s, of its CN (i.e., of the n value). An increase in the uranium oxidation state (from two to six) is accompanied by a regular decrease in the volume of the corresponding VDP from 14.9 to 9.2 µ³. One can see from Table 3 that similar regularity is generally exhibited by the total VDP surface area. At the same time, contrary to V_VDP, the volume of the corresponding coordination polyhedron considerably increases with an increase in the CN at a fixed oxidation state (Table 1), and its average value does not correlate with the uranium oxidation state (Table 3).

When analyzing pair interatomic interactions, modern crystallochemistry, as a rule, deals with one-dimensional characteristics (atomic radii and interatomic distances); Table 3 presents the one-dimensional analog of the average VDP volume for each uranium valence state. As an analog, we used the radius of a spherical domain (R_SD), which is numerically equal to the radius of the sphere whose volume is equal to the volume of the corresponding VDP. In other words, R_SD characterizes the sphere into which an uranium VDP of arbitrary shape would transform if the oxygen atoms generated a spherically symmetrical mean crystal field. Interestingly, in three known modifications of metallic uranium, the average R_SD value [1.73(3) µ, Table 3] coincides with the uranium Slater radius 1.75 µ to within s [9]. A regular decrease in R_SD with the increase in the oxidation state of uranium atoms (Table 3) may be considered, by analogy with the known fact that the effective ionic radius of atom A decreases with increasing x (A), as a result of the increase in the electron density transfer from the metal atom to the electron-accepting atoms of its first coordination sphere.

An additional analysis showed that, for the U (IV-VI) atoms in the oxygen environment, the x(U) values are linearly related to the R_SD values,

x (U) = 29.17(7) - 17.88(5)R_SD,                           (3)

It is of interest to consider the compounds with fractional oxidation states of uranium in terms of relationship (3). U₃O₈ is the classical example of such compounds. The question as to which of the two alternative formulas (specifically, U⁴⁺U₂⁶⁺O₈ or U⁶⁺U₂⁵⁺O₈) more adequately describes the valence state of the uranium atoms in the structure still remains to be solved [10]. By now, the structures of a (at room temperature [II] and 500C [12]) and b [13] modifications have been determined (structures 1, II, and III, respectively). All notations we used completely coincide with those used in [11-13], according to which structures I, II, and III contain two, two, and three crystallographically independent sorts of uranium atoms, respectively, with CN 6 or 7 and tetragonal- or pentagonal-bipyramidal coordination polyhedra, respectively. In this connection, note that the CN_VDP coincides with CN_CLASS for all uranium atoms, except for U(l) in structure II. The VDP of this atom shows the presence of the additional U(l)-O(3) contact (3.14 µ), which was disregarded in the classical description of II (Table 4); therefore, the CN of U(l) increases to 7 (or 6+1), and the coordination polyhedron of this atom should be considered as a pentagonal rather than tetragonal bipyramid.

Note that, although the coordination polyhedra of two sorts of uranium atoms in structure I considerably differ from one another in the interatomic U-O distances for the equatorial plane of the UO₇ pentagonal bipyramids (Table 4), the VDP volumes of these atoms are almost the same. It then follows from the preceding that the uranium atoms in structure I are in the same valence state. Contrary to I, the crystallographically inequivalent sorts of uranium atoms in structures II and III noticeably differ not only in the r(U-O) values, but also in the V_VDP values (Table 4). Therefore, the uranium atoms in these structures can be considered to be in different valence states. Table 4 gives the values of x (U) for the uranium atoms in structures I-III calculated by equation (3). Note that, although the value of V_VDP of the uranium atoms in the three U₃O₈ structures changes over a rather wide range from 8.95 to 10.30 µ³, the mean value of V_VDP of the uranium atom is virtually constant (9.65, 9.67, and 9.67 µ³ for I, II, and III, respectively).

Table 4. Some characteristics of the uranium atoms in the structure of U₃O₈

In our opinion, this fact indicates that V_VDP is an integral characteristic that is rather sensitive to a change in the valence state of uranium atoms, since in the compound with fixed chemical composition the increase in the oxidation state of some of the atoms (and, hence, the decrease in their V_VDP or R_SD) must be inevitably accompanied by an equivalent decrease in the oxidation state (i.e., an increase in V_VDP or R_SD) of the other part of the atoms. Therefore, it is not surprising that, although the calculated x (U) values in structures I-III change from 5.0 to 6.1 (Table 4), their summarized values per formula unit U₃O₈ are almost the same (16.8, 16.5, and 16.6, respectively). In our opinion, this is in satisfactory agreement with the theoretical value 16. In I-III, s (R_SD) s (R(U-O)) 0.02 µ, and the error in determining x (U) by equation (3) is about 0.5. This fact and the data in Table 4 allow one to suggest that, in the structures of the U₃O₈ modifications, 5 x (U) 6; for I and II, the formula should be written as U₃^5.33+O₈, and for III, U⁶⁺U₂⁵⁺O₈. Note that this inference is consistent with the results of quantum chemical calculations of the electron-density disproportionation in uranium oxygen-containing compounds (including U₃O₈), which were recently obtained in terms of the Xa -SW method [14].

1. Wells, A.F., Structural Inorganic Chemistry, Oxford: Clarendon, 1962, 3rd ed.

2. Galiulin, R.V., Kristallograficheskaya geometriya (Crystallographic Geometry), Moscow: Nauka, 1984.

3. lvanenko, A.A., Blatov, V.A., and Serezhkin, V.N., Kristallografiya, 1992, vol. 37, no. 6, p. 1365.

4. Serezhkin, V.N., Blatov, V.A., and Shevchenko, A.P., Koord. Khim., 1995, vol. 21, no. 3, p. 163.

5. Blatov, V.A., Shevchenko, A.P., and Serezhkin, V.N., Zh. Strukt. Khim., 1993, vol. 34, no. 5, p. 183.

6. Blatov, V.A. and Serezhkin, V.N., Available from VINTII, 1989, Moscow, no. 7303-V89.

7. Charpin, P., Falcher, G., Nierlich, M., et al., Acta Crystallogr.. Sect. C: Cryst. Struct. Commun., 1990, vol. 46, no. 10, p. 2775.

8. Barret, SA., Acta Crystallogr., Sec. B: Struct. Sci., 1982, vol. 38, no. 11, p. 2775.

9. Sovremennaya kristallografiya (Modem Crystallography), Vainshtein, B.K., Fndkin, V.M., and Indenborn, V.L., Eds., Moscow: Nauka, 1979, vol. 2.

10. lonova, G.V. and Kiseleva, A.A., Zh. Neorg. Khim., 1994, vol. 39, no. 8, p. 1373.

11. Loopstra, B.O., Acta Crystallogr., 1964, vol. 17, no. 6, p. 651.

12. Herak, R.,Acta Crystallogr., Sect. B: Struct. Sci., 1969, vol. 25, no. 12, p. 2505.

13. Loopstra, B.O., Acta Crystallogr., Sect. B: Struct. Sci., 1970, vol. 26, no. 5, p. 656.

14. lonova, G.V. and Kiseleva, A.A., Zh. Neorg. Khim., 1994, vol. 39, no. 8, p. 1377.

15. Zakharov, L.N., Saf'yanov,Yu.N., and Domrachev, G.A., Problemy kristallokhimii (Problems of Crystal Chemistry), Porai-Koshits, M.A., Ed., Moscow: Nauka, 1990, p. III.

16. Zefirov, Yu.V., Kristallografiya, 1994, vol. 39, no. 6, p. 1025.

17. Zorkii, P.M., Zh. Fiz. Khim., 1994, vol. 68, no. 6, p. 966.

18. Shevchenko, A.P., Blatov, VA., and Serezhkin, V.N., Dokl. Akad. Nauk SSSR, 1992, vol. 324, no. 6, p. 1199.