Samara State University, Samara, Russia

Abstract - The geometric characteristics of Voronoi-Dirichlet polyhedra (VDP) for 354 U(VI) atoms in the structures of oxygen-containing compounds are established. It is shown that the volumes of VDPs, as distinct from the volumes of the corresponding coordination polyhedra, are virtually independent of the coordination numbers of uranium atoms and are on average 9.18(25) µ³. The results obtained are in agreement with the previously suggested model of deformable spheres describing the packing of structural units in uranium(VI) compounds.

The calculation of characteristics of the VDPs of U(VI) atoms in the structures of oxygen-containing compounds, including uranyl complexes and simple and mixed oxides (uranates), was carried out by the structurally topological TOPOS software [6]. These programs make it possible to calculate atomic VDPs in crystal structures of any degree of complexity. The original information on crystal structures contained in the Cambridge crystallographic databank and the databank for uranyl compounds [7] was used in the calculations, provided that three conditions were fulfilled: (1) the crystal structure was determined with R_f 0.10; (2) in accordance with the classical description, the UO_n polyhedra occur in the structure; and (3) statistically disordered uranium and oxygen atoms are not in the structure. The data on the structure of 276 compounds, which contain 354 crystallographically different sorts of uranium atoms in their structures, satisfied the requirements indicated. Hydrogen atoms exist in 236 of the 276 compounds; however, their coordinates were determined in the structures of only 95 compounds. Considering that the accuracy of the determination of the coordinates of hydrogen atoms in the presence of a uranium atom is low and that the positions of these atoms were not established in the structures of 141 compounds, the hydrogen atoms were disregarded in the calculations of the VDPs of uranium atoms.

Table 1. Characteristics of the dual coordination polyhedra of U(VI) atoms at K_d(U-O) 0.5

Notes:

In accordance with the data obtained (Table 1), the dual CPs of uranium atoms have from 6 to 12 faces at any K_d(U-O) < 0.5. For a particular compound, the variation of K_d(U-O) within the range 0 < K_d(U-O) < 0.5 affects only the absolute values of the volume (V_S) and total area of faces (S_S) of dual CPs. The dual CPs themselves are similar to each other, with the coefficient of similarity being equal to the ratio between the corresponding values of K_d, and thus have identical combinatorial and topological characteristics. Because each face corresponds to a single U-O bond, the CPs of uranium atoms have composition UO_n, where n= 6, 1, 8, 9, 10, or 12 at K_d(U-O) < 0.5 (Table 1). As an example. Table 2 gives the results of calculation of the VDPs of uranium atoms for the structures NaCa₃UO₂(CO₃)₃SO₄F Ç l0H₂O [8] and K₂UO₂(SO₄)₃ [9], in which the uranium atoms have coordination numbers 8 and 7.

Note that, in accordance with the classical method of determination of coordination numbers considered above, the coordination numbers of U(VI) atoms in oxygen-containing compounds vary from 6 to 8 [2]. In this case, the atomic CPs have the form of a tetragonal, pentagonal, or hexagonal bipyramid. The results that we obtained testify that U atoms, as expected, have dual CPs in the form of a tetragonal, pentagonal, or hexagonal prism at K_d(U-O) 0.5 in most of the compounds studied; that is, in 347 cases out of 354, the coordination numbers of the U atoms equal 6, 7, or 8, respectively, as in the classical approach.

The results obtained (Table 1) are also indicative of the occurrence of six compounds, in the structure of which seven crystallographically different sorts of uranium atoms display abnormally high coordination numbers (in comparison with the classical values): 9, 10 (in five cases), and 12. According to available data (as an example, Table 3 presents the results of the calculation of VDPs of uranium atoms in two "abnormal" compounds, namely, b-CdUO₄ [10] and UO₂(C₄H₄O₅) [11]), an increase in the coordination number is due to the occurrence of two, four, or six U O contacts with interatomic distances (from 3.12 to 3.83 µ) approximately 1.5-2 times longer than those typical for U(VI) [2]. VDPs in the form of a distorted tetragonal or pentagonal prism with several additional small faces correspond to all of the abnormal coordination numbers (9, 10, or 12) of uranium atoms; the VDPs of uranium atoms corresponding to coordination number 9 = 7 + 2, 10 =6+ 4, and 12=6+6 have two, four, and six additional faces of this type, respectively. The faces of dual CPs corresponding to such contacts (Table 3) have areas that do not exceed 3% of S_S. The smallest solid

Table 2. Results of the calculations of the VDPs of uranium atoms in the structures of uranium(VI) compounds*

* In the r(U-X) column, the distance is shown between the central uranium atom and the atom whose designation and coordinates are given in the corresponding line of the table: S_SEG is the value of the area of the dual CP face common to the central atom and the atom shown in the line, expressed in % of the total area; W is the solid angle of the dual CP face common to the central atom and the atom shown in the line, expressed in % of the total solid angle 4p steradian of the uranium atom.

Table 3. Results of the calculation of the VDPs of uranium atoms in the structures of "abnormal" uranium(VI) compounds*

angles, not exceeding 2.5% of the total solid angle of the uranium atom (4p steradian), also correspond to these faces. Recall that a certain solid angle (W ), which is numerically equal to the area of a segment of a sphere of unit radius (with the center at the uranium atom) cut by the pyramid with the uranium atom in the apex and the corresponding face of the polyhedron in the base, corresponds to each face of the VDP of the A atom [4]. We believe that the solid angles are more important geometric characteristics of dual CPs, because unlike V_S and S_s which change their absolute values with the variation of K_d(A-X), the solid angles of the faces are invariant with respect to the transformation of similarity as long as the combinatorially topological structure of the polyhedron does not change with the variation of K_d. In totality, the data available make it possible to suggest that all of the U-O contacts with W < 0.2p steradian [r(U-O) > 3 µ] correspond to additional non-valent long-range action, which was not found in the traditional method of the determination of atomic coordination numbers. The supplementary analysis shows that analogous abnormal contacts with r(U-O) > 3.0 µ and W (U-O)< 0.2p steradian occur in the dual CPs of five uranium atoms. Although the values of coordination numbers found for these dual CPs (7 and 8 for one and four compounds, respectively) coincide with well-known values, they must be considered as 6+1 and 7 + 1 from the classical point of view.

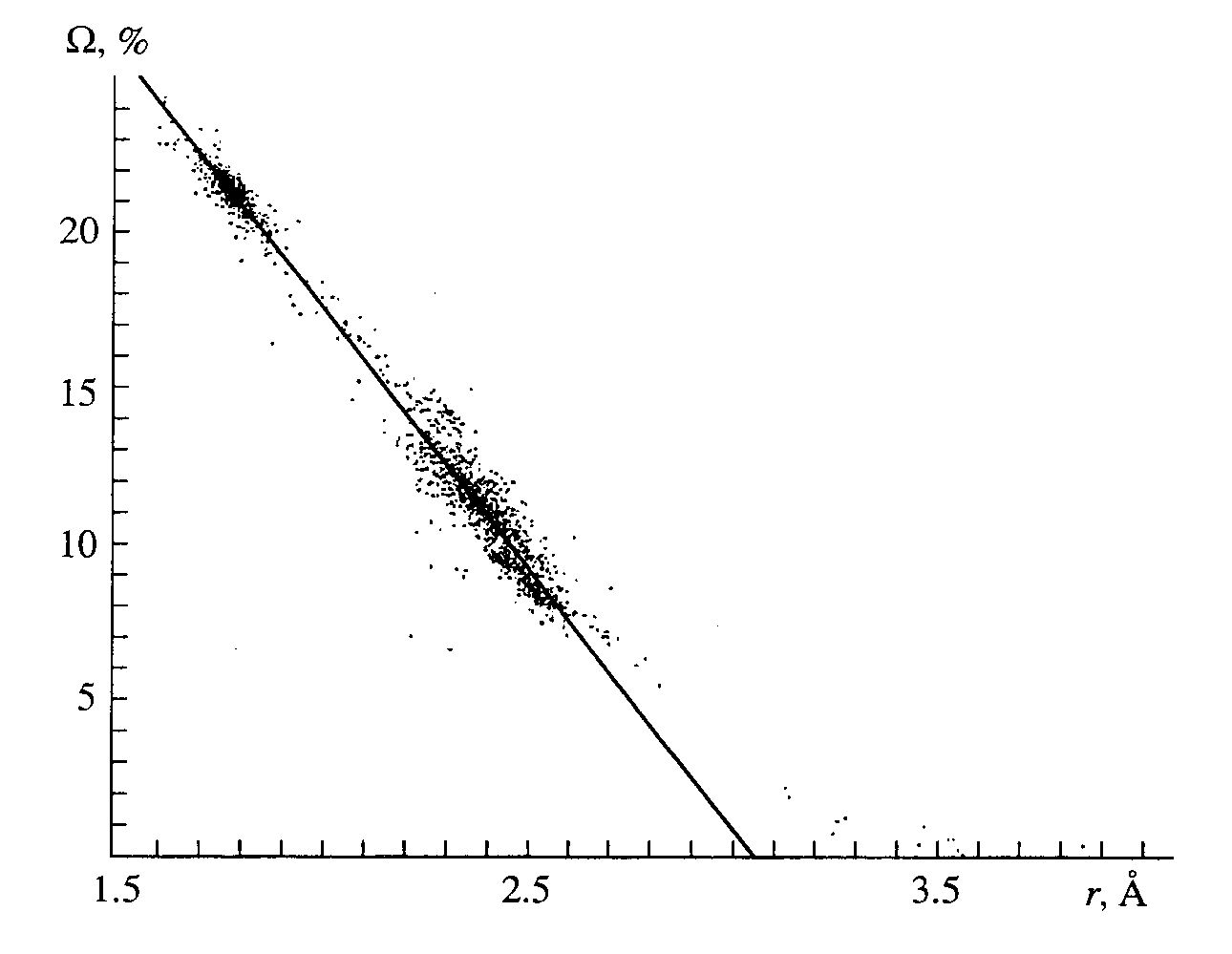
Note in this connection that the experimental values of r(U-O) and W (U-O) corresponding to all of the abnormal interactions at r(U-O) > 3 µ fall in the right nonlinear portion of the curve that describes the dependence of W (U-O) on r(U-O) in the VDPs of 354 uranium atoms in the structures of the compounds under discussion (Fig. 1). Contrary to the abnormally large distances, the values of r(U-O), which are considered as strong chemical bonds (covalent or polarized cova-lent) in the classical description of the structure of U(VI) compounds, lie in a straight line (Fig. 1), which may be expressed using the least-squares method as

W (U-O) = 51.2(1)- 16.79(5)r(U-O) (1)

with the coefficient of correlation 0.991 for 2549 experimental points at r(U-O) < 3 µ. In equation (1) and in Fig. 1, the values of W (U-O) are expressed as percents of the total solid angle (4p steradian) of the uranium atom, and r(U-O) are given in µ. The linear form of the function W (r) may be explained using the following approximations: (a) For the CP AX_n, all of the distances from the A atom to the vertices of the dual CP are equal, that is, the dual CP is inscribed in the sphere of radius R with the center at the atom A. (b) The radii of the circumscribed spheres R are equal for all types of dual CPs, regardless of the coordination number of the A atom. (c) Each pyramid with the A atom at the apex that is based on the face of the dual CP corresponding to the A-X contact is approximated by a cone that has the area of its base equal to the area of the pyramid's face, and the length of its generator is R.

Fig. 1. Relationship between the solid angles of faces and r(U-O) in 354 VDPs of the U(VI) atoms.

W (A-X) = 50 – 50 r_f /R (2)

W (A-X) = 50 – 25 r(A-X)/R. (3)

For the sampling considered, the value of R averaged over all of the VDPs of 354 uranium atoms is 1.72(4) µ; that is, the above-mentioned approximations (a) and (b) may be considered true. Some deviations in the values of coefficients in equations (1) and (3) are determined by the fact that the approximation (c) is rather rough. We believe that a small scatter in the values of R(s = 0.04 µ) for the VDPs of uranium atoms suggests that the model considering the crystal structure of the uranium-containing compounds as a packing of deformable spheres [12] is correct. We emphasize especially that the plot shown in Fig. 1 is fully reproduced at any value of K_d(U-O) within the range 0 < K_d(U-O) 0.5 because of similarity between the dual CPs of uranium atoms.

According to the data obtained (Table 4), in the dual CPs of uranium atoms at K_d(U-O) 0.6, supplementary faces generally appear that correspond to nonvalent contacts U-X (X are atoms of the second coordination sphere) in addition to the faces corresponding to U-O bonds. The nature and total number of X atoms at fixed K_d(U-O) 0.6 depend on the chemical composition and crystal structure of the compound. For a particular compound (some examples are given in Tables 2 and 3), the number of faces of the U-X type increases (generally to 18) as K_d(U-O) increases from 0.5 to 0.8.

Table 4. Characteristics of the dual coordination polyhedra of U(VI) atoms at K_d(U-O) 0.6*

Fig. 2. Relationship between the solid angles corresponding to the faces of 354 dual CPs in UO_nX_m and r[U-O(X)] at K_d= 0.8.

The solid angles W (U-X) of the faces that appear increase with increasing K_d(U-O) as a result of both a decrease in the solid angles of the faces of the U-O type (Table 2) and the disappearance of some faces of such type, starting with those that correspond to W (U-O) < 0.2p steradian (Table 3) even at K_d(U-O) 0.5. As may be seen from Fig. 2 or from examples in Tables 2 and 3, the faces with the values of W (U-O) achieving 15 - 20% of the total solid angle of 4p steradian correspond to covalently bonded oxygen atoms of the first coordination sphere in the dual CP of composition UO_nX_m (4 n 8 and 0 m 18) even at K_d(U-O) = 0.8. Further analysis shows that, in spite of the wide variety of the composition (Table 4) and form of the dual CP of compounds UO_nX_m, rather compact regions of values correspond to X atoms of a particular chemical sort in the plot of the relationship between W (U-X) and r(U-X). As an example. Fig. 3 displays the fragment of Fig. 2 showing the relationship between W (U-X) and r(U-X) only for X = O or S at K_d(U-O) = 0.8 in all of the sulfurcontaining uranium compounds (32 out of 276 compounds) used in the calculations.

Fig. 3. Relationship between the solid angles corresponding to the faces of 99 dual CPs in UO_nX_m and r[U-O(S)] at K_d = 0.8.

The results presented above (Table 4) make it possible to suggest that all of the faces of the A-X type of the dual CP of a certain atom A at W (A-X) > 0.2p steradian correspond to valence contacts A-X (that is, to strong chemical bonds) in the structure of any compound at K_d(A-X) 0.5. If this suggestion, which possibly requires a refinement of the threshold value of W (A-X), is confirmed for other inorganic and coordination compounds, the direct calculation of the geometric characteristics of the dual CP at K_d = 0.5 for any bonds will make it possible to determine the classical value of the coordination number of any A atom in the structure without using any information about the radii of atoms in the compound.

In the calculation of characteristics of the dual CP, the choice of constant value K_d = 0.5 for all of the bonds is determined by the following reasons. First, only at K_d = 0.5 are dual CPs coincident with VDPs, which are capable of filling three-dimensional space without hollows; at any K_d 0.5, the partition of the space by a procedure analogous to the construction of VDPs generally gives rise to simply connected spatial regions of points, which do not belong to any of the dual CPs. Second, for the heteronuclear bonds A-X, there is no criterion for choosing a "correct" K_d for a given pair of atoms. The use of any crystalline atomic radii for this purpose leaves the problem unsolved, because, as noted above, the concept of a radius itself is, to a great extent, a matter of convention, and it is not clear a priori which system of radii should be used for a particular pair of A and X atoms in the structure of a specific compound. Third, any value of K_d 0.5 taken as a "correct" one for a particular A-X bond is strictly correct only at a single point Z corresponding to the intersection of this bond with the plane normal to it, because the value of K_d equals the ratio of the lengths of the AZ and AX segments. For any other point of this plane (for example, P), the AP : PX ratio will differ from the predetermined value AZ/ZX = K_d( 1 – K_d) and will depend on the length of the ZP segment. At the same time, the solid angles of the faces of any dual CP calculated at 0 < K_d < 0.5 coincide because of similarity to those calculated for the VDP of the same atom, i.e., at K_d= 0.5.

The data obtained (Tables 1 and 4) show that, at any fixed value of K_d(U-O), the volumes of the dual CPs (V_S) of U(VI) atoms are equal within the limits of twice the mean square deviation and are independent of the uranium coordination number. Thus, the mean volume of the VDP (V_VDP), that is, V_S at K_d = 0.5, of a uranium(VI) atom in the polyhedra UO_n for 354 crystallographically different sorts of atoms equals 9.18(25) µ³. If only the dual CPs in which the number of oxygen atoms coincides with the classical coordination number of U(VI) (i.e., only the dual CPs of UO_n or UO_nX_m types with n = 6, 7, or 8, which are appropriate to no less than 347 of 354 uranium atoms at any K_d 0.8) are taken into account, the corresponding values of V_S overlap even within 1s (V_S). This fact is especially remarkable because the volumes of the corresponding classical CPs (Table 1) increase significantly as the coordination numbers of uranium atoms increase. At any given value of K_d(U-O), the total area of the faces of the dual CP and VDP (S_S and S_VDP), the mean value of which equals 25.8(5) µ² for 354 VDPs, is found to be constant (within 2s, Tables 1 and 4), as are V_S and V_VDP of the uranium(VI) atom. Note that the values of V_S and V_VDP (or S_S and S_VDP) given in Tables 1 and 4, in accordance with [4], are not the absolute characteristics of the regions of action of uranium atoms and are important only for comparison analysis, because the ratio of the volumes or surface areas of any two bodies are invariant with respect to similarity transformation.

1. Sovremennaya Kristallografiya (Modern Crystallography), Vainshtein, B.K., Fridkin, V.M., and Indenborn. V.L., Eds., Moscow: Nauka, 1979, vol. 2.

2. Blatov, V.A. and Serezhkin, V.N. Radiokhimiya, 1991, vol. 33, no. 1, p. 14.

3. Wells, A.F., Structural Inorganic Chemistry, Oxford: Clarendon, 1984,5th ed.

4. Ivanenko, A.A., Blatov, V.A., and Serezhkin, V.N„ Kristallografiya, 1992, vol. 37, no. 6, p. 1365.

5. Bader, R., Chemical Application of Topology and Graph Theory, King, R„ Ed., Amsterdam: Elsevier, 1983.

6. Blatov, V.A., Shevchenko, A.P., and Serezhkin, V.N., Zh. Strukt. Khim., 1993, vol. 34, no. 5, p. 183.

7. Blatov, V.A. and Serezhkin, V.N., Available from VINITI, 1989, no. 7303-V89.

8. Mereiter, K., Tschermaks Mineral. Petrogr. Mitt., 1986, vol. 35, no. 1, p. 1.

9. Mikhailov, Yu.N., Kokh, L.A., Kuznetsov, V.G., el al., Koord. Khim., 1977, vol. 3, no. 4, p. 508.

10. Yamashita, T., Fujino, T., Masaki, N„ et al., J. Solid State Chem., 1981, vol. 37, no. 1, p. 133.

11. Bombieri, G., Croatto, U., Graziani, R., et al., Acta Crystallogr., Sect. B: Struct. Sci., 1974, vol. 30, no. 2, p. 407.

12. Shevchenko, A.P., Blatov, VA., and Serezhkin, V.N„ Dokl. Ross. Akad. Nauk, 1992, vol. 324, no. 6, p. 1199.