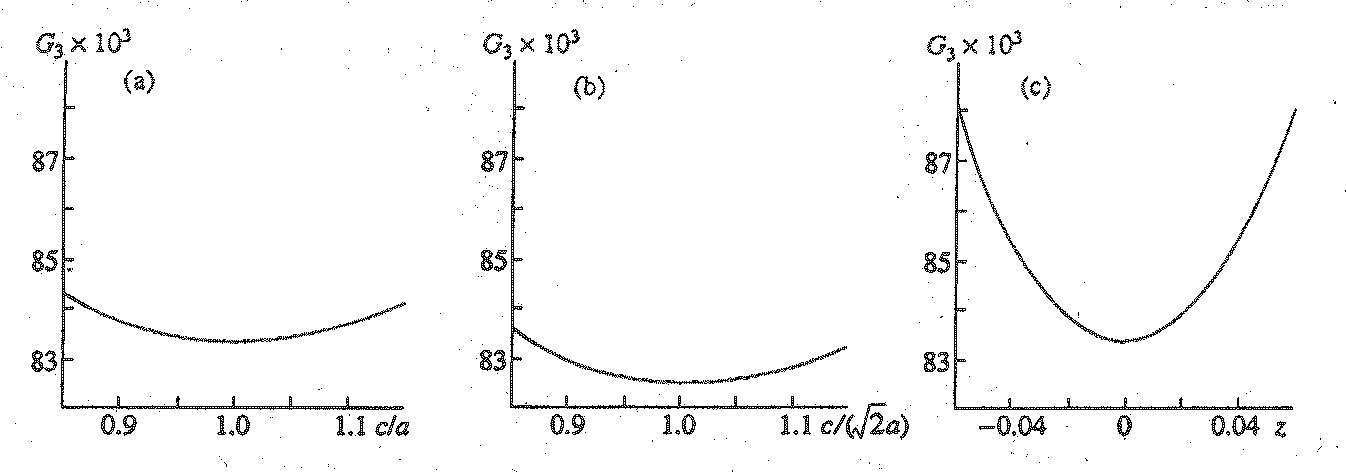
Crystallography Reports Vol. 39. No. 3. 1994. pp. 402 - 408 Translated from Kristallografya, Vol. 39, No. 3. 1994. pp. 457-463 . Original Russian Text Copyright
Ó 1994 by Blatov, Pol'kin, Serezhkin.Polymorphism of Elementary Substances and the Principle of Uniformity
V.A.BIatov,V.A.Pol'kin, and V.N.Serezhkin
Samara State University, Samara, Russia
Received June 28, 1993; in final form, November 10, 1993
Abstract - The problem of quantitatively estimating the uniformity of crystalline structures is discussed. The root-mean-square error (G3 of the quantizer corresponding to the lattice of gravity centers of a crystal's structural units was put forward as a criterion for the uniformity. The mentioned characteristic is shown to consider specific features of the lattice uniformity in a more detailed way than the known criteria. Analyzing structures of elementary systems shows that the uniformity changes under thermal phase transitions and depends on the position of an element in the Periodic Table. The value of G3 was suggested to serve as a semiquantitative estimation of the ratio of contributions from directed and undirected interactions into the total crystal energy.
Geometric analysis of a crystal structure is now one of the main methods used in crystal chemistry to explore a solid. Within the framework of this approach, the continuous crystal space is replaced by a discrete (point) one, and the geometric properties of a set of points are analyzed. These points represent centers of gravity of electron density maxima or of structural units (atoms or groups of atoms). The mentioned set (multiregular system) is a set of N regular point systems (where N is the number of crystallographically independent structural units) and is a particular case of Delone systems [1]. One can treat a multiregular system as a kind of "response function", bearing in mind that its shape is determined by a complicated atomic interaction that cannot be described in detail at present. Numerous investigations showed that the geometric and topological properties of the multiregular system are connected with a number of energetic characteristics of a crystal. In particular, the strength of atomic interaction can be estimated from the values of interatomic distances, and the crystal lattice energy can be estimated from the relative positions of points (in the case of ionic crystals) [2], etc. However, we think that it is necessary to look for new criteria that will characterize the multiregular system and, therefore, be connected with the physicochemical properties of a crystal.
According to the described approach, we neglect specific features of electron density distribution in the crystal space and consider only geometrical and topological properties of the corresponding multiregular system. In particular, we employ the traditional classification of pairwise atomic interactions: they can be directed (covalent) and undirected (ionic, metallic, and van der Waals bonds). Interactions can differ in strength: covalent, metallic, and ionic bonds are strong; van der Waals bonds are weak. We intentionally do not consider electron properties of chemical bonds, bearing in mind that the data on band structure is now scarce and contradictory even for elementary substances [3]. Further, we recognize the local and global geometrical and topological properties of a multiregular system. Local properties are intrinsic in a finite subset of an infinite multiregular system. They include characteristics that are well known in crystal chemistry, such as interatomic distances, valence and dihedral angles, coordination numbers and polyhedra, point symmetry, etc. Global properties characterize a multiregular system as a whole (they include space symmetry, the type and density of sphere packing corresponding to the structure, topology of interatomic bonds, etc.). At present, crystallochemical analysis deals mainly with the local properties of multiregular systems. This investigation is the continuation of our work (begun in [4]) aimed at elaborating the methods of numerical analysis of the global geometrical and topological properties of a crystal lattice, which is mathematically interpreted as a multiregular system.
Under the influence of central forces of attraction, atoms and more complex structural units are known to arrange themselves so as to maximize the number of short contacts between them (the principle of maximum space filling [2]). On the other hand, if repulsion forces of an analogous nature are present, atoms and atomic groups tend to arrange themselves so that the distances between them are as great as possible. Thus, the two-dimensional model (arrangement of negative charges on a sphere), which is used in the Gillespie theory [5] in particular, yields a uniform distribution of like charges on a spherical surface.
A three-dimensional crystal structure forms as a result of the superposition of interatomic attraction and repulsion forces. Within the central force approximation, one can suppose that, similar to the two-dimensional model, the minimum lattice energy is reached with the most "uniform" space arrangement of atoms or structural groups and that the multiregular system will exhibit the global property of uniformity. In this connection, it should be noted that the problem of the uniform distribution of points in space was discussed in [6]. As a criterion for uniformity, the authors of [6] suggested the value of coverage (Kc) of space by equal, intersecting spheres centered at the points of the system in question. According to [6], the minimum coverage corresponds to the most uniform system of points. Among three-dimensional periodic structures, such a system is represented by the body-centered cubic (bcc) lattice, which is characterized by Kc = 1.4635 [7]. Another criterion for uniformity can be formulated using parameters of discreteness (r, the minimum distance between points of the system) and coverage (R, the maximum distance from any point of space to the nearest point of the system) employed in the theory of Delone systems [1]. As a quantitative estimation, one can use the ratio R/r, the minimum value of which corresponds to the most uniform system of points. For three-dimensional periodic lattices, the minimum value R/r = 0.646 is also reached in the case of the bcc lattice [1].
Fig. 1. Variation of the g3 value: (a) for a tetragonal prism, depending on the ratio of its height (c) to the length (a) of the base edge; (b) for a tetragonal bipyramid, depending on ratio c/(
Note that the aforementioned criteria for uniformity hold only for a limited number of multiregular systems in which all points are crystallographically equivalent. For crystals consisting of atoms of more than one crystallographic type, variations in the form and dimensions of atomic regions of action should be considered (i.e., sets of points influenced more by the given atom than by any other atom of the structure). In the structure of elementary substances' crystals consisting of atoms of single chemical type (and up to eight crystallographic types, as in the case of Se structure), atomic regions of action are known to be represented by the corresponding Voronoi-Dirichlet polyhedra (further designated as VDP). All the points of these polyhedra are located closer to the given atom than to any neighboring one.
We suggest using an estimation of the root-mean-square error of quantizer [7] as a semiquantitative criterion for the uniformity of any multiregular system. Quantizer is a lattice superimposed on the continuous space so that the coordinates of any space point are rounded off to the coordinates of the nearest point of the lattice (Pi). Thus, all the points within the VDP of point Pi [P(Pi)] are taken equal to Pi,. The error of quantizer is measured by the distance from Pi to the point whose coordinates are rounded off. To quantitatively express the error of quantizer, we use an estimation of the average value of root-mean-square error normalized to space dimensionality (n) and volume (V) of VDP [7):
In the examples considered below, we take quantizer to coincide with the multiregular system. Then, M is the number of basis atoms in an elementary cell; r is the distance from a point of VDP P(Pi) to the corresponding atom (this atom corresponds to point Pi of the multiregular system).
In particular, if a point of the multiregular system coincides with the center of gravity of its VDP, the value of Gn is equal to the dimensionless second moment of inertia of the polyhedron [7]. The quantizer with the most uniform arrangement of points with respect to the space has the minimum value of Gn. In three-dimensional space, the best of the known lattice quantizers is the bcc lattice [7], for which G3 = 0.07854.
The value of G3 is an integral, parameter that takes into account a number of the multiregular system's characteristics connected with its uniformity. In considering some of them, we will employ the usual crystal chemistry terminology.
Table 1. Values of G3 and R/
r for regular polyhedra and a spherePolyhedron |
R/r |
G3� 103 |
Tetrahedron |
3.000 |
104.00 |
Cube |
1.732 |
83.33 |
Octahedron |
1.732 |
82.55 |
Dodecahedron |
1.258 |
78.13 |
Icosahedron |
1.258 |
77.82 |
Sphere |
1.000 |
76.97 |
(1) Spread in values of interatomic distances in the. coordination polyhedron of an atom. These distances are equal to twice the minimum distances from this atom to faces of the corresponding VDP. As an example, Fig. la presents the dependence of (G3 of a VDP (which has the form of a square prism), on the ratio of its height (c) to the length of the base edge (a). From Fig. 1a, one can see that the minimum value (G3 = 0.08333 corresponds to the ratio
?/? = 1, under which the VDP of the atom transforms into a cube, and all six distances in the atomic coordination polyhedron (octahedron) are equal. The increasing or decreasing c/a ratio with respect to the mentioned value results in a tetragonal distortion of the octahedron and gives rise to four nearer (coordination 4+2) or four farther (coordination 2+4) neighbors in the atomic coordination sphere, respectively. This results in increasing G3.(2) Spread in distances from atoms (which are treated as contacting hard spheres) to the centers of the structure voids (i.e., vertices of VDP). To illustrate the influence of this factor, we will consider a VDP in the form of a tetragonal bipyramid with the variable ratio
?/? (where ? is the bipyramid height; a is the length of its base edge). Such a VDP corresponds to the tetragonal-prismatic surrounding of the central atom. In this case, all the distances from the central atom to the eight atoms of its first coordination sphere are equal under any value of ?/?, whereas the spread in distances to the centers of voids (i.e., to the six bipyramid vertices) depends on this ratio. From Fig. 1b, one can see that the minimum value of G3 (0.08255) corresponds to the VDP in the form of a regular octahedron (?/? = 1.414).(3) Ratio R/
r , where R and r are radii of the spheres that are circumscribed about and inscribed into a VDP, can serve as an estimate of the polyhedron sphericity; this is because, in the limiting case, a polyhedron with an infinite number of faces equidistant from the central atom degenerates into a sphere, for which the R/r value is minimum and equals unity. One can observe the correlation between the second moment of a VDP and ratio R/r in a row of Plato bodies (Table 1). All the faces and vertices of these bodies are equivalent, and the above-considered criteria 1 and 2 fail to yield any differences in the uniformity of structures that involve polyhedra of this kind. It is worth noting that dual polyhedra are characterized by the same value of R/r (Table 1), whereas values of G3 are regularly diminished as the number of the polyhedron's faces is increased.(4) The central atom displacement from the VDP center of gravity. As an example, consider a cubic VDP in which the central atom is displaced by a distance ? (expressed in units of
the cube edge) from the center of gravity to one of the faces. Analyzing the dependence of G3 on z (Fig. 1c) shows that the most uniform surrounding of the central atom is attained at z = 0 and, as �z� � 0.5, the value of G3 is sharply increased.The examples given show that the G3 characteristic considers specific features of the multiregular system uniformity in more detail than any of the aforementioned parameters. The criterion demanding the minimum ratio of 'the coverage parameter (R) to the discreteness parameter (r) for structures with atoms of one crystallographic type is, in fact, analogous to the above-considered factor 3 (because r= 2
r) and, consequently, is a component of the G3 characteristic. In turn, the criterion demanding the minimum of R/r value also demands the minimum of Kc (and the maximum of the packing coefficient Kp) becauseFor brevity, we will further discuss the structure uniformity, that is, the uniformity of the corresponding multiregular system.
We employ the value of G3 to analyze how the crystal structure of elements changes under thermal phase transitions (Table 2) and how it depends on the position of the element in the Periodic Table (Table 3, Figs. 2 and 3). Calculations were performed taking into account formula (1) and using the DIRICHLET program realized within the framework of the TOPOS program complex [8]. The error in calculating G3 values caused by errors of the structural experiment was no more than 0.01%.
As can be seen from Table 2, in the high-temperature modifications of elementary substances, the structure uniformity increases (the value of G3 decreases) with temperature in practically all cases (including the case of a long sequence of phases such as
a-Pu-� -e-Pu). The only exceptions are modifications that are metastable under the conditions of the structural experiment (such as b-Mn, b-W, and the low-temperature modification of Ga). Note an interesting detail: for Mn and W, the stable a -modification is more uniform than the metastable one, whereas the situation is inverse for gallium modifications.For metals not presented in Table 2, polymorphous transitions follow two schemes:
(a) a close-packed (fcc, hcp) structure
� the bcc lattice;(b) hcp (fcc)
� fcc(hcp).In the first case, the uniformity, is regularly increased (e.g., the G3 value is decreased from 0.07878 to 0.07854 for beryllium), and in the second case (in particular, for gadolinium), the values of G3 for the two modifications coincide within the degree of accuracy and equal 0.07874. Relatively small changes in G3 for different modifications of most metals (usually within 1-2%) point to the domination of central forces in the interatomic interaction in their structure.
The above-cited data leads to the conclusion that, under a thermal phase transition, the high-temperature phase is more uniform than the low-temperature one. This can be attributed to the increase in the contribution of undirected interactions to the total lattice energy with increasing temperature and energy of atomic thermal motion.
We considered the dependence of the G3 values of atoms in the structure of elements on their position in the Periodic Table. From Tables 2 and 3 and Fig. 2, one can see that in any subgroup of the Periodic Table, the structure uniformity usually increases (G3 decreases) as the atomic number of the element is increased. In the subgroup of alkali metals, the structure uniformity does not change when passing from lithium to cesium. In the beryllium subgroup, the uniformity is slightly increased (the values of G3 are equal to 0.07878 and 0.07854 for Be and Ra structures, respectively). The only exception is the boron subgroup, where the nonmonotonic character of the changing G3 value is caused by the absence of covalent interactions in aluminum structure.
It is worth noting that the value of G3 can serve as a semiquantitative estimate of the ratio of contributions from directed and undirected interactions to the total crystal energy. The obtained results (Table 2) show G3<0.0820 for substances with predominant metallic bonds without pronounced anisotropic interactions. This limit also holds for crystals of inert gases, in which the main role is played by van der Waals interactions. On the other hand, G3>0.0820 for crystals with a considerable covalent interatomic interaction. Thus, the aforementioned value separates crystals with the domination of undirected bonds and crystals with pronounced directed interatomic interactions.
However, we failed to obtain a clearly defined dependence of G3 on the topology of. the. network of covalent bonds. G3 varies from 0.08225 (iodine) to 0.09503 (nitrogen) in the case of crystals built of molecular groups; from 0.08384 (tellurium) to 0.08852 (selenium) in the case of chain groups; from 0.08375 (antimony) to 0.11204 (graphite) in the case of layered groups; and from 0.08333 (polonium) to 0.09667 (boron) in the case of skeleton groups. Accordingly, the value of G3 does not enable us to determine uniquely the cumber of covalent bonds per atom in a structure. This fact causes the uniformity of elements' structures to change in periods in a more complex way than
in subgroups (Fig. 3). There are two opposite trends. On one hand, the uniformity of structures must decrease with weakening metal properties of elements in a period. On the other hand, in nonmetals of groups ? - VIII of the periodic Table, according to the Hume-Rothery rule, the number of covalent bonds formed by every atom decreases and, at the same time, spherically symmetric (van der Waals) interactions begin to play a greater role as a period progresses. This causes G3 to decrease. As a result, the maximum nonuniformity corresponds to groups IV, V, and VI (Fig. 3), and the most uniform structure is typical of alkali metals (primarily, metallic bond) and inert gases (practically only van der Waals interactions).
Table 2. Values of G3 for polymorphous modifications of some of the metals
Polymorphous modification |
Temperature, � ? |
G3 � 103 |
Polymorphous modification |
Temperature, � ? |
G3 � 103 |
a -Ga |
* |
85.67 |
a -Pu |
<121 |
80.67 |
b -Ga** |
-163 |
81.01 |
b -Pu |
121-205 |
79.09 |
a -Mn |
<707 |
78.94 |
g -Pu |
205-315 |
78.90 |
b -Mn** |
25 |
79.21 |
d -Pu |
315-468 |
78.74 |
g -Mn |
1085-1100 |
78.74 |
d '-Pu |
468-481 |
78.56 |
g '-Mn |
1100-1137 |
78.74 |
e -Pu* |
>481 |
78.54 |
d -Mn* |
>1137 |
78.54 |
a -Sn |
<13 |
91.15 |
a -Np |
<278 |
81.00 |
b -Sn |
>13 |
81.10 |
b -Np |
278-540 |
79.51 |
a -U |
<660 |
79.43 |
g -Np* |
>540 |
78.54 |
b -U |
660-760 |
78.83 |
a -Po |
<75 |
83.33 |
g -U* |
>760 |
78.54 |
b -Po* |
>75 |
81.86 |
a -W |
* |
78.54 |
b -W** |
650 |
78.74 |
Table 3. Values of G3 for structures of some of the elements
Element* |
G3 � 103 |
Element* |
G3 � 103 |
B(trigonal) |
96.67 |
Ge(diamond type) |
91.15 |
C(graphite) |
112.04 |
As(grey) |
84.38 |
N( a ) |
95.03 |
Se(monoclinic) |
88.52 |
O( a ) |
92.25 |
Br |
83.36 |
F( a ) |
86.72 |
Sb(rhombohedral) |
83.75 |
Si(diamond type) |
91.15 |
Te(trigonal) |
83.84 |
P(orthorhombic) |
87.02 |
I |
82.25 |
S(orthorhombic) |
91.51 |
Bi(rhombohedral) |
83.72 |
Cl |
84.27 |
Po( a ) |
83.33 |
Note: *Modification is indicated in brackets.
Table 4. Results of calculating atomic VDP for bromine, selenium, arsenic, and germanium structures using the DIRICHLET* program
Central atom: Br 1 0.500 0.390 0.135 S = 56.459 |
Central atom: Se 1 0.584 0.315 0.437 S = 56.850 |
||||||||||||||||||||||||||
No. |
Atom |
x |
y |
z |
Dist. |
SSeg. |
BAng. |
No. |
Atom |
x |
y |
z |
Dist. |
SSeg. |
BAng. |
||||||||||||
1 |
Br1 |
0.500 |
0.610 |
-0.135 |
2.268 |
20.06 |
24.29** |
1 |
Se2 |
0.477 |
0.227 |
0.246 |
2.301 |
20.87 |
24.04** |
||||||||||||
2 |
Br1 |
0.500 |
0.110 |
-0.365 |
3.313 |
13.91 |
13.80 |
2 |
Se8 |
0.710 |
0.479 |
0.334 |
2.337 |
16.78 |
21.97** |
||||||||||||
3 |
Br1 |
0.500 |
0.110 |
0.635 |
3.313 |
13.91 |
13.80 |
3 |
Se7 |
0.840 |
0.254 |
0.632 |
3.703 |
6.81 |
6.88 |
||||||||||||
4 |
Br1 |
0.500 |
0.610 |
0.865 |
3.792 |
9.47 |
8.79 |
4 |
Se3 |
0.328 |
0.398 |
0.240 |
3.739 |
2.70 |
2.18 |
||||||||||||
5 |
Br1 |
1.000 |
0.610 |
0.365 |
3.983 |
4.89 |
4.63 |
5 |
Se7 |
0.660 |
0.754 |
0.368 |
3.740 |
2.70 |
2.19 |
||||||||||||
6 |
Br1 |
0.000 |
0.610 |
0.365 |
3.983 |
4.89 |
4.63 |
6 |
Se7 |
0.340 |
0.246 |
0.632 |
3.749 |
10.17 |
9.05 |
||||||||||||
7 |
Br1 |
1.000 |
0.390 |
-0.365 |
4.017 |
5.50 |
5.07 |
7 |
Se1 |
0.416 |
0.685 |
0.563 |
3.902 |
7.91 |
7.27 |
||||||||||||
8 |
Br1 |
0.000 |
0.390 |
-0.365 |
4.017 |
5.50 |
5.07 |
8 |
Se3 |
0.672 |
0.602 |
0.760 |
3.914 |
6.96 |
6.50 |
||||||||||||
9 |
Br1 |
1.000 |
0.390 |
0.635 |
4.017 |
5.50 |
5.07 |
9 |
Se5 |
0.590 |
0.169 |
0.843 |
3.956 |
8.98 |
7.73 |
||||||||||||
10 |
Br1 |
0.000 |
0.390 |
0.635 |
4.017 |
5.50 |
5.07 |
10 |
Se3 |
0.828 |
0.102 |
0.240 |
4.095 |
4.81 |
4.11 |
||||||||||||
11 |
Br1 |
1.000 |
0.110 |
0.135 |
4.133 |
5.0? |
4.57 |
11 |
Se8 |
0.790 |
-0.021 |
0.666 |
4.277 |
4.60 |
3.60 |
||||||||||||
12 |
Br1 |
0.000 |
0.110 |
0.135 |
4.133 |
5.05 |
4.57 |
12 |
Se7 |
0.660 |
-0.246 |
0.368 |
4.683 |
4.84 |
3.39 |
||||||||||||
13 |
Br1 |
0.500 |
0.390 |
-0.865 |
4.480 |
0.39 |
0.32 |
13 |
Se6 |
0.590 |
-0.160 |
0.142 |
4.719 |
0.10 |
0.07 |
||||||||||||
14 |
Br1 |
0.500 |
0.390 |
1.135 |
4.480 |
0.39 |
0.32 |
14 |
Se2 |
0.523 |
-0.227 |
0.754 |
5.358 |
1.32 |
0.77 |
||||||||||||
15 |
Se1 |
0.416 |
-0.315 |
0.563 |
5.671 |
0.46 |
0.26 |
||||||||||||||||||||
Central atom: As 1 0.333 0.667 0.441 S = 45.238 |
Central atom: Ge 1 0.750 0.750 0.750 S = 50.066 |
||||||||||||||||||||||||||
No. |
Atom |
x |
y |
z |
Dist. |
SSeg. |
BAng. |
No. |
Atom |
x |
y |
z |
Dist. |
SSeg. |
BAng. |
||||||||||||
1 |
As1 |
0.667 |
1.333 |
0.559 |
2.506 |
17.92 |
19.05** |
1 |
Ge1 |
1.000 |
0.500 |
0.500 |
2.450 |
20.76 |
22.04** |
||||||||||||
2 |
As1 |
-0.333 |
0.333 |
0.559 |
2.506 |
17.92 |
19.05** |
2 |
Ge1 |
0.500 |
1.000 |
0.500 |
2.450 |
20.76 |
22.04** |
||||||||||||
3 |
As1 |
0.667 |
0.333 |
0.559 |
2.506 |
17.92 |
19.05** |
3 |
Ge1 |
1.000 |
1.000 |
1.000 |
2.450 |
20.76 |
22.04** |
||||||||||||
4 |
As1 |
1.000 |
1.000 |
0.226 |
3.137 |
12.42 |
11.80 |
4 |
Ge1 |
0.500 |
0.500 |
1.000 |
2.450 |
20.76 |
22.04** |
||||||||||||
5 |
As1 |
0.000 |
0.000 |
0.226 |
3.137 |
12.42 |
11.80 |
5 |
Ge1 |
1.250 |
0.750 |
0.250 |
4.000 |
1.41 |
0.99 |
||||||||||||
6 |
As1 |
0.000 |
1.000 |
0.226 |
3.137 |
12.42 |
11.80 |
. 6 |
Ge1 |
0.750 |
1.250 |
0.250 |
4.000 |
1.41 |
0.99 |
||||||||||||
7 |
As1 |
1.333 |
1.667 |
0.441 |
3.760 |
1.47 |
1.22 |
7 |
Ge1 |
0.250 |
0.750 |
0.250 |
4.000 |
1.41 |
0.99 . |
||||||||||||
8 |
As1 |
-0.667 |
-0.333 |
0.441 |
3.760 |
1.47 |
1.22 |
8 |
Ge1 |
0.750 |
0.250 |
0.250 |
4.000 |
1.41 |
0.99 |
||||||||||||
9 |
As1 |
0.333 |
-0.333 |
0.441 |
3.760 |
1.47 |
1.22 |
9 |
Ge1 |
1.250 |
1.250 |
0.750 |
4.000 |
1.41 |
0.99 |
||||||||||||
10 |
As1 |
1.333 |
0.667 |
0.441 |
3.760 |
1.47 |
1.22 |
10 |
Ge1 |
0.250 |
0.250 |
0.750 |
4.000 |
1.41 |
0.99 |
||||||||||||
11 |
As1 |
0.333 |
1.667 |
0.441 |
3.760 |
1.47 |
1.22 |
11 |
Ge1 |
1.250 |
0.250 |
0.750 |
4.000 |
1.41 |
0.99 |
||||||||||||
12 |
As1 |
-0.667 |
0.667 |
0.441 |
3.760 |
1.47 |
1.22 |
12 |
Ge1 |
1.250 |
0.750 |
1.250 |
4.000 |
1.41 |
0,99 |
||||||||||||
13 |
As1 |
0.000 |
0.000 |
0.774 |
4.132 |
0.03 |
0.02 |
13 |
Ge1 |
0.750 |
1.250 |
1.250 |
4.000 |
1.41 |
0.99 |
||||||||||||
14 |
As1 |
1.000 |
1.000 |
0.774 |
4.132 |
0.03 |
0.02 |
14 |
Ge1 |
0.250 |
1.250 |
0.750 |
4.000 |
1.41 |
0.99 |
||||||||||||
15 |
As1 |
0.000 |
1.000 |
0.774 |
4.132 |
0.03 |
0.02 |
15 |
Ge1 |
0.250 |
0.750 |
1.250 |
4.000 |
1.41 |
0.99 |
||||||||||||
16 |
As1 |
0.667 |
1.333 |
0.107 |
4.132 |
0.03 |
0.02 |
16 |
Ge1 |
0.750 |
0.250 |
1.250 |
4.000 |
1.41 |
0.99 |
||||||||||||
17 |
As1 |
0.667 |
0.333 |
0.107 |
4.132 |
0.03 |
0.02 |
||||||||||||||||||||
18 |
As1 |
-0.333 |
0.333 |
0.107 |
4.132 |
0.03 |
0.02 |
||||||||||||||||||||
19 |
As1 |
0.333 |
0.667 |
0.893 |
4.768 |
0.04 |
0.02 |
||||||||||||||||||||
Fig.2. G3 values for structures of elements of (a) III, (b) IV, (c) V, (d) VI, and (e) VII principal subgroups of the Periodic Table.
Fig.3. Dependence of the G3 value on an element's atomic number (N) in structures of elementary substances.
We should note that, given the VDP form, one can often distinguish the contacts corresponding to weak van der Waals interactions from strong covalent bonds in nomnetallic structures. According to [10], VDP faces with greater values of surface and solid angle correspond to strong covalent bonds. As an example. Table 4 cites the results of calculating (with the help of the DIRICHLET program) the structures of germanium, arsenic, selenium, and bromine, characterized by a skeleton, layered, chain, and molecular composition, respectively. From Table 4, one can see that, in any of the aforementioned structures, solid angles of faces are equal (or close to one another, as in the structure of selenium) for VDP of atoms corresponding to covalent contacts. These angles are at least one and a half times as great as those corresponding to nonvalence interactions.
We think that the results obtained enable us to put forward the following principle of crystal-lattice uniformity: in a thermodynamically stable structure, atoms and groups of atoms interacting in an undirected fashion tend to arrange themselves in space so that the system of their centers of gravity ensures the. minimum value of G3. In our opinion, the principle of uniformity supplements the principle of maximum space filling [2] and is based on the same physical foundation. We expect the principle of uniformity to hold for polymorphic rows of more complex heterodesmic compounds as well. In the latter case, however, the tendency toward uniform distribution appears to be typical of structural groups rather than individual atoms.
REFERENCES