


Next: Parameters and Variables
Up: LEAST SQUARES REFINEMENT USING
Previous: LEAST SQUARES REFINEMENT USING
The term LSQ is used here to mean Least Squares Refinement ,
which uses
observations of a function to improve the values of some set of
parameters on which that function depends.
Refinement involving a crystal structure could be either standard single
crystal LSQ
refinement, in which each observation depends on a single
structure factor, or profile refinement (PR) for which
several structure factors contribute to one observation.
The PR routines are written to use many of the same CCSL routines as do
standard LSQ
main programs. The PR programs and Libraries are available separately, with
a separate Manual.
CCSL also deals with simpler LSQ problems. For example, the main program
FWLSQ fits the 5,7 or 9 parameters of the exponential approximation to a
scattering factor curve. The simplicity in this case is that no crystal structure is
involved.
Another simple case is the refinement of (up to) 6 cell parameters,
given an observed list of d-spacings (actually d* squared values, in
the main program DSLSQ). This must deal with
the constraints which are
necessarily imposed on the cell parameters by the space group symmetry.
The essentials of a LSQ problem are:
- a)
- a set of observations of something,
(the observed function )
usually with their estimated standard deviations,
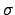 's,
measured at different values of some argument ARG ;
ARG may be
's,
measured at different values of some argument ARG ;
ARG may be 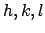 (for standard LSQ),
(for standard LSQ),
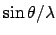 ,
,
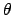 (for
Rietveld PR) or
(for
Rietveld PR) or 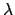 , or energy, or time of flight; it is a
quantity which takes different values, and will identify the
observation.
, or energy, or time of flight; it is a
quantity which takes different values, and will identify the
observation.
For crystallographic applications the observations are often all of the
same physical thing, but this is not necessary. For example, geometric
constraints may be introduced by giving bond lengths and/or angles as
additional types of observation, with 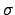 's.
's.
- b)
- some calculated function involving ARG ,
which defines a
mathematical model to be compared with an observation. This calculated
function depends on parameters , things which may possibly be varied in order
to improve the fit of the function to its related observations.
By fit we mean minimisation of the weighted sum of squares of
differences
between observed and calculated function values (where the summing is
over the different values of ARG ). It is desirable to use
statistical weights (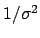 )
for the differences.
)
for the differences.
The theory may be viewed as using the beginning of a Taylor series
expansion, and therefore requires that the parameters be close to
their correct values, making the required shifts so small that their
squares may be neglected.



Next: Parameters and Variables
Up: LEAST SQUARES REFINEMENT USING
Previous: LEAST SQUARES REFINEMENT USING
P.J. Brown - Institut Laue Langevin, Grenoble, FRANCE. e-mail brown@ill.fr