Modulated crystal structures belong to that kind of crystal structures, in which atoms suffer from fluctuations in position, occupation and/or thermal motion. If the period of fluctuation matches that of the three-dimensional unit cell then a superstructure results, otherwise an incommensurate modulated structure is obtained.
        A modulated structure can be regarded as the result of applying a periodic modulation to a regular structure. Figure 1 shows two examples. The modulation wave in figure 1a represents the fluctuation of atomic occupancy. When it is applied to the regular structure, the ‘heights’ of the atoms are modified. A commensurate modulated structure (superstructure) will result (figure 1b), if the period T of the modulation function matches the period t of the structure, i.e. T/t = n, where n is an integer. The resulting superstructure now has a true period T and a pseudo period t, respectively corresponding to a true unit cell and a pseudo unit cell. On the other hand, if T does not match t (figure 1c), i.e. T/t = r, where r is not an integer, we obtain an incommensurate modulated structure, in which no exact periodicity can be found although t remains a pseudo period. A modulation function can also represent the fluctuation of atomic position as well as thermal motion. These kinds of modulation may also be either commensurate or incommensurate. In practice a modulated structure may simultaneously include different kinds of modulation.

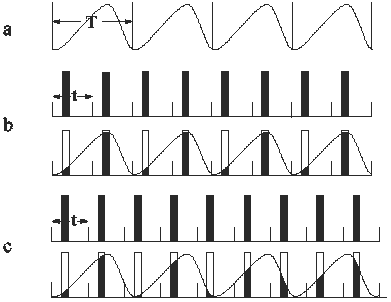
Figure 1. Occupational modulation of a one-dimensional structure

(a) modulation wave with a period equal to T; (b) upper row: one-dimensional regular structure with atoms shown as thick vertical lines and with a period equal to t; lower row: the resulting commensurate modulated structure; (c) upper row: one-dimensional regular structure; lower row: the resulting incommensurate modulated structure.

       Incommensurate modulated crystals yield 3-dimensional diffraction patterns, which contains satellites round the main reflections. An example of a section of such a 3-dimensional diffraction pattern is shown schematically in Figure 2.

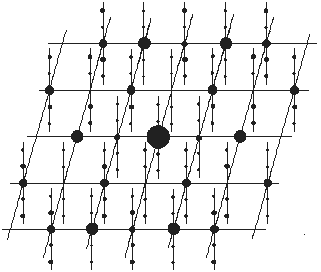
Figure 2. Schematic diffraction pattern of an incommensurate modulated structure. The vertical line segments indicate projected lattice lines parallel to the fourth dimension.

The main reflections are consistent with a regular 3-dimensional reciprocal lattice but the satellites do not fit the same lattice. On the other hand, while the satellites does not match the main lattice, they have their own periodicity. Hence, it can be imagined that the 3-dimensional diffraction pattern is a projection of a 4-dimensional reciprocal lattice, in which the main and the satellite reflections are all regularly situated at the lattice nodes. From the properties of the Fourier transform the incommensurate modulated structure here considered can be regarded as a 3-dimensional “section” of a 4-dimensional periodic structure. The above example corresponds to a one-dimensional modulation. For an n-dimensional (n=1,2, …) modulation, it needs a (3+n)-dimensional description. For details of superspace symmetry the reader is referred to the papers cited below.
        There is a special kind of incommensurate modulated structures called composite structures. The characteristic of which is the coexistence of two or more mutually incommensurate 3-dimensional lattices. Owing to the interaction of coexisting lattices, composite structures are also incommensurate modulated structures. Unlike ordinary incommensurate modulated structures, composite structures do not have a 3-dimensional average (basic) structure. The basic structure of a composite structure corresponds to a 4- or higher-dimensional periodic structure. For a detailed description of composite structures the reader is referred to the paper by van Smaalen (1992).

References
         De Wolff, P. M. (1974). The pseudo-symmetry of modulated crystal structures, Acta Cryst. A30, 777-785.
         De Wolff, P. M. Janssen, T. and Janner, A. (1981). The superspace groups for incommensurate crystal structures with a one-dimensional modulation, Acta Cryst. A37, 625-636.
         Yamamoto, A. (1982). Structure factor of modulated crystal structures, Acta Cryst. A38, 87-92.
         Janner, A. Janssen, T. and De Wolff, P. M. (1983). Bravais classes for incommensurate crystal phases, Acta Cryst. A39, 658-666.
         Jansen, T., Janner, A., Looijenga-Vos, A. and De Wolff, P. M.  (1992). Incommensurate and commensurate modulated structures, in Wilson, A. J. C. (ed.), International Tables for Crystallography, Kluwer Academic Publishers, Dordrecht, pp. 797-835; 843-844.
         Van Smaalen, S. (1992). Superspace description of incommensurate intergrowth compounds and the application to inorganic misfit layer compounds, Mater. Sci. Forum 100 & 101, 173-222.