The VHS video: "Texturing of Rocks in the Earth's Mantle. A Convection Model Based on Polycrystal Plasticity" by Hans-Rudolf Wenk, Paul Dawson, Chris Pelkie and Yvan Chastel is now available for distribution by the Am. Geophys. Union and can be ordered at the following address:
http://earth.agu.org/cgi-bin/agubookstore?memb=agu&topic=..SP&book=SESP0522946&cart=96365&search=
![]()
![]()
Texturing of Rocks in the Earth’s Mantle.
A Convection Model Based on Polycrystal Plasticity.
H.-R. WENK, Department of Geology and Geophysics, University of California, Berkeley CA 94720
P.R. DAWSON, Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca NY 14853
C. PELKIE, Cornell Theory Center, Cornell University, Ithaca NY 14853
Y. CHASTEL, Ecole des Mines, Sophia Antipolis, France
Why did we prepare this video?
Anisotropy in the Earth is becoming an important issue in geophysics. The underlying causes, deformation of crystals by intracrystalline processes are very complex and difficult to approach by scientists who are not polycrystal plasticity experts. With this video which illustrates basic concepts in a simplified manner, we would like to introduce non-experts to this fascinating branch of science. Since anisotropy development is a very dynamic process, an animated movie is an ideal way to illustrate this.
The video is meant for geophysicists, seismologists and geologists and can be used in corresponding courses. The content is also relevant for materials scientists by illustrating micro-macro linking for a very large heterogeneous system. The following introduction gives instructors and students some background information and directs those to the pertinent literature who want to study the subject in greater depth.
Introduction to the subject of anisotropic convection
The upper mantle has fascinated geologists and geophysicists alike. This part of the Earth undergoes intense deformation which is expressed on all scales, from intracrystalline deformation features in olivine to large scale seismic anisotropy. It is an excellent example to illustrate the relationship between microscopic processes at the atomic scale and macroscopic properties, relying on polycrystal plasticity theory developed by materials scientists. An animated video introduces, on an introductory level, concepts of deformation, development of preferred orientation, heterogeneous flow in a convection cell and resulting seismic anisotropy. During convection in the Earth’s mantle, deformation of crystals produces preferred orientation of olivine that is the primary cause for seismic anisotropy.
Seismologists documented a directional dependence in the propagation of waves generated by earthquakes [4-10]. Waves travel about 10% more rapidly perpendicular to ocean ridges than parallel to them over distances comparable to dimensions of continents. Anisotropy on such a large scale originates in the directional properties of the rock-forming minerals and the corresponding deformations that induce texture. In this context the term "texture" is used synonymously with the term "lattice preferred orientation" and describes the orientation distribution of crystals in a polycrystalline aggregate.
Microscopic processes occurring within crystals are responsible for macroscopic anisotropic properties of materials. These relationships have been quantified and comprise the core of modern texture analysis [1]. The Earth is a very heterogeneous and dynamic system at all scales. Deformation occurs at the large macroscopic level on the scale of continents, down to the atomic structure within crystals.

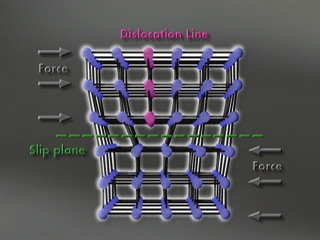
Heterogeneous Earth structure - - - - - - - - - - - - - - - Dislocation in a crystal lattice
Due to this complexity there is limited utility in modeling deformation using approaches that are restricted to the macroscopic scale wherein the mantle is treated as a continuum. Instead, the video illustrates an approach that combines models from two scales.
(a) At the macroscopic level the finite element method is ideally suited to deal with the heterogeneous deformation patterns and to resolve gradients in the flow field associated with deformation [14-15].
(b) At the microscopic level, polycrystal plasticity theory simulates deformation processes within crystals [1-3].
These processes intimately link the properties of rock's constituent minerals with the Earth's structural formations. Rocks are polyphasic, and comprised of minerals that, individually, are often strongly anisotropic and may differ substantially in strength. Deformation by intracrystalline slip, often accompanied by dynamic recrystallization, is the single most important factor in establishing the crystallographic texture. The rotation of crystal lattices accompanies deformation by slip, owing to the limited number of discrete slip systems (on rational slip planes and in rational slip directions).
We apply two-dimensional finite element methods and polycrystal plasticity theory to model deformation in the solid upper mantle of the Earth. The upper mantle is largely composed of the orthorhombic magnesium silicate mineral olivine Mg2SiO4 and deforms by convection, driven by temperature gradients. There is upwelling of buoyant material along ridges and downwelling of dense material in subduction zones. Finite element simulations indicate that during convection, crystals indeed reorient into characteristic textures that cause anisotropic physical properties [16-18]. These patterns are highly heterogeneous over the span of the convection cell and depend on the specific straining history along individual streamlines of the cell. The rotations that reorient crystal lattices are due to activation of slip systems in deforming single crystals as well as the macroscopic rotation of material progressing along a streamline. Both of these are most intense during upwelling at ridges and during subduction.
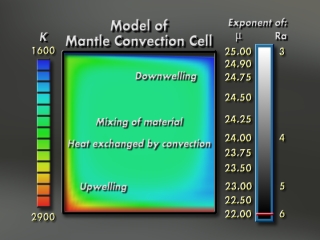
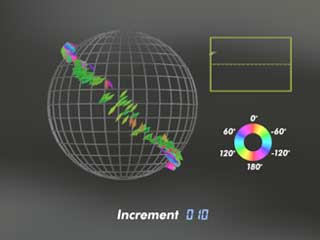
Thermal convection for large Rayleigh numbers - - - - - Crystal orientations during upwelling
From the simplified model, it is evident that the mantle is not a structure-less viscous medium but shares many properties with a single crystal which displays internal structure and anisotropy. There are structural variations that vary both laterally and with depth as expressed in pole figures.

Simulated preferred orientation patterns of olivine in the upper mantle. Upwelling on left side.
These findings are of significant interest for seismologists, geodynamicists and structural geologists who recognize the importance of anisotropy. The link between the crystal properties and structural features of a geological formation is evident: anisotropy in the mechanical properties of rocks influences their deformations, and the deformations themselves induce the texture that is the source of anisotropy in the properties. The mechanical anisotropy from texture is a primary source of direction dependence observed in the seismic wave propagation. Other potential sources are oriented fractures or compositionally layered structures [6] but crystallographic preferred orientation is recognized as a major factor. Using the crystallographic texture throughout the convection cell and the physical properties of single crystals, seismic velocity averages over mantle sectors can be computed and the directional dependence of wave propagation can be determined. The predicted azimuthal variation of p-wave anisotropy of 5-10% in the model (curve) agrees well with actual observed values (red dots) [8]. Recent applications to flow at mid-ocean ridges help to distinguish between passive and buoyancy-enhanced upwelling [16]. The video only shows results for longitudinal (p) wave velocities. Clearly shear waves (s) and shear wave splitting [10] play an important role in the investigation of anisotropy in the Earth.
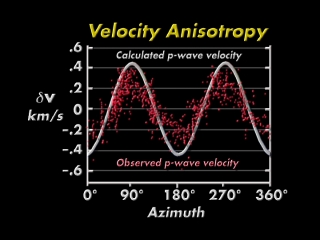
Azimuthal variation of seismic anisotropy. Red dots observed [8], white line simulated.
The video illustrates the general features one may expect during mantle deformation. It emphasizes processes, relationships, not details. A more realistic model would have to be extended to take into account the three-dimensional Earth [13], of second phases and phase transformations, particularly in the transition zone [12], interaction with the crust, e.g. during subduction [11], and would need to include processes of dynamic recrystallization [3]. These are all very exciting fields of future studies in geodynamics. By including polycrystal plasticity, geophysical deformation modeling is entering a new state of refinement and is an excellent example for quantitative texture analysis.
![]()
Selected Reading
Polycrystal plasticity
1. Kocks U.F., Tomé C.N. & Wenk H-R (1998). Texture and Anisotropy. Preferred Orientation in Polycrystals and their Effect on Material Properties. Cambridge Univ. Press.
2. Wenk, H.-R. (1999). A voyage through the deformed Earth with the self-consistent model. Model. and Simul. Mat. Sci. Engin. (in press)
3. Wenk, H.-R. & Tomé, C.N. (1999). Modeling dynamic recrystallization of olivine aggregates deformed in simple shear. J. Geophys. Res. (in press).
Seismic anisotropy
4. Ben Ismail, W.& Mainprice, D., An olivine fabric database: an overview of upper mantle fabrics and seismic anisotropy, Tectonophysics, 296, 145-158, 1998.
5. Christensen, N.I.(1984). The magnitude, symmetry, and origin of upper mantle anisotropy based on fabric analyses of ultramafic tectonites, Geophys. J. Roy. Astron. Soc., 76, 89-111.
6. Crampin, S. (1981). A review of wave motion in anisotropic and cracked elastic media. Wave Motion 3, 242-391.
7. Hess, H.H. (1964). Seismic anisotropy of the uppermost mantle under oceans, Nature, 203, 629.
8. Morris, G. B., Raitt, R. W. & Shor, G. G. (1969). Velocity anisotropy and delay time maps of the mantle near Hawaii. J. Geophys. Res., 74, 4300-4316.
9. Nishimura, C. & Forsyth, D. (1989). The anisotropic structure of the upper mantle in the Pacific. Geophys J. 96, 203-229.
10. Silver P.G. (1996). Seismic anisotropy beneath the continents: Probing the depths of geology. Ann. Rev. Earth Planet. Sci. 24, 385-432.
Mantle dynamics
11. Ringwood, A.E. (1990). Slab-mantle interactions. Chem. Geol. 82, 187-207.
12. Schubert, G., Yuen, D.A. & Turcotte, D.L. (1975). Role of phase transformations in a dynamic mantle. Geophys. J. R. Astr. Soc. 42, 705-735.
13. Tackley, P.J. (1996). Effects of strongly variable viscosity on three-dimensional compressional convection in planetary mantles. J. Geophys. Res. 101, 3311-3332.
Anisotropic finite element method
14. Beaudoin, A.J., Mathur, K.K., Dawson, P.R., Kocks, U.F. & Korzekwa, D.A. (1994). Application of polycrystal plasticity to sheet forming. Computer Methods in Applied Mechanics and Engineering, 117, 49-70.
15. Sarma, G.B. & Dawson, P.R. (1996). Effects of interaction among crystals on the inhomogeneous deformations of polycrystals. Acta mater. 44, 1937-1953.
Anisotropic mantle convection
16. Blackman, D.K., Kendall, J.M., Dawson, P.R., Wenk, H.R., Boyce, D. & Morgan, J.P. (1996). Teleseismic imaging of subaxial flow at mid-ocean ridges: travel time effects of anisotropic mineral texture in the mantle. Geoph. J. Int. 127, 415-426.
17. Chastel Y.B., Dawson P.R., Wenk H.-R. & Bennett K. (1993). Anisotropic convection with implications for the upper mantle. J. Geophys. Res. B98, 17757-17771.
18. Dawson P.R. & Wenk H.-R. (1999). Texturing of the upper mantle during convection. Phil. Mag. (in press).
![]()
Last Edited 09/23/99