Kalpha-1
The 3 "if" :
Then we could simulate a Kalpha-1 powder pattern, add to it some
statistical noise, then simulate the Kalpha-2 component, then add the two
patterns and compare...
Mathematically, the two patterns should be equivalent, because of the 3 "if" above (a coded text can be exactly decoded - without any information loss - if you have the code key), and a Rietveld refinement on both patterns should lead to equivalent results.
Let us try.
The calculation of the 2 powder patterns was done by the Fullprof program on a small-size orthorhombic cell, that of GaOOH :
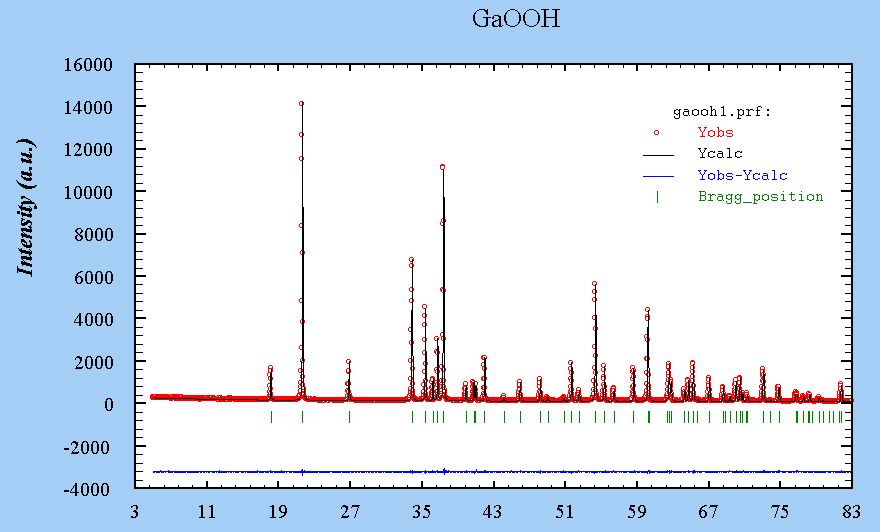
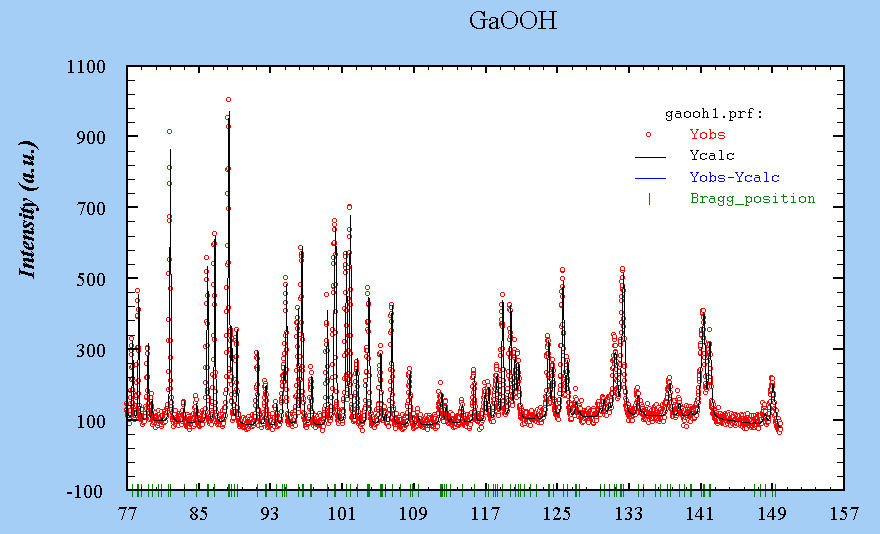
Kalpha-1


See the refinement results in the Fullprof .sum file. Download the .dat file and the .pcr file.
Kalpha-1-2
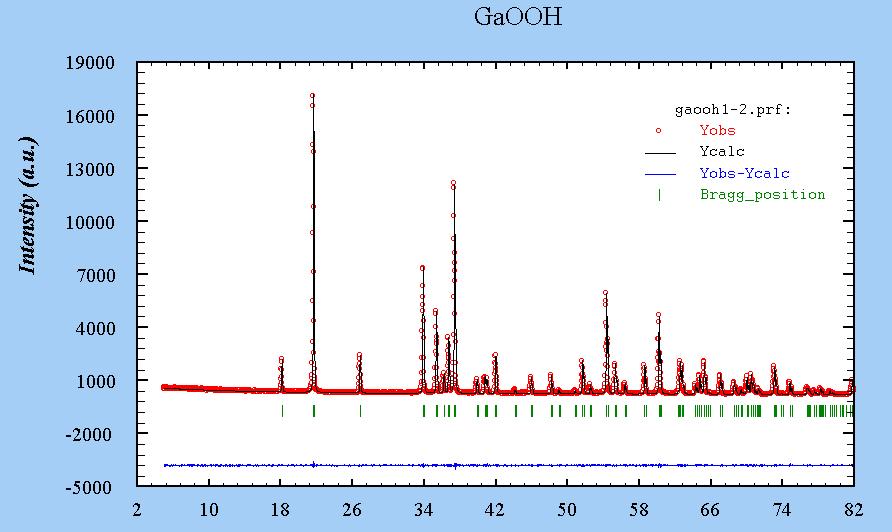

See the refinement results in the Fullprof .sum file. Download the .dat file and the .pcr file.
Conclusion
So what ? Compare the Fullprof .sum files above, do you find any clear difference in the refinements ? There is not. Try a larger cell with thousand reflections will not change anything, if the 3 "if" above are really mathematically/physically true.
Of course, the problem here is that the 3 "if" above are not completely true...
However, this is not a reason for trusting only your eyes, telling that Kalpha-1 is so much better, this would also not be completely the truth.
If the 3 "if" were true, we could perfectly remove the Kalpha-2 component (in case of extremely good statistics, anyway), but we cannot. Nevertheless, we can almost do it, with only some ripple problems, right ? And this is why we prefer to make the Rietveld refinement on the original pattern, but not on the pattern corrected from the Kalpha-2 component : less errors occur when adding the alpha-1 and alpha-2 calculated contributions than when stripping alpha-2 from the observed pattern. Anyway, a primary beam monochromator is nothing else than a Kalpha-2 stripping hardware. Some are not better in that exercise than certain Kalpha-2 stripping software, and may let up to 1.5% of alpha-2 residue on your experimental powder pattern. Of course, if you want your Kalpha-2 stripping sofware to make well the job, you should have a high-resolution pattern, with a counting step sufficiently small, and a quite good counting statistics.
A Kalpha-1 pattern and a Kalpha pattern are almost equivalent. You will not obtain easier indexation from a Kalpha-1 pattern than from a Kalpha pattern corrected from the Kalpha-2 component. And the final Rietveld refinements would be quite similar, in spite of what say your eyes.
Do not believe only your eyes.
Armel Le Bail
October 2000