INTRODUCTION by EXAMPLES
To summarize :
The well known Rietveld
method is a crystal structure refinement method, from powder diffraction
data.
A pattern is calculated from a series of structural parameters (cell, atomic coordinates, thermal motion, etc) and peak shape and width parameters (plus background, Lorentz-polarisation correction, etc), and compared to the observed data.
Parameters are adjusted
by a least-square process.
An example : two samples
of NiF2.
One is well crystallized
and the other was submitted to ball milling.
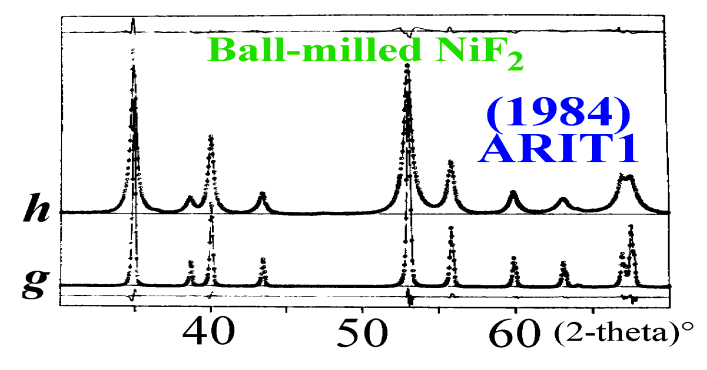
Profile shapes and widths
of the well crystallized sample are due to the instrumental effects (noted
g).
Those of the ball-milled
sample show additional broadening effects. The experimental pattern (noted
h)
being the convolution of an effect due to the sample (noted f) by
the instrumental effect (g):
h = f *
g
Do not confuse deconvolution with desummation (like Ka2 stripping).
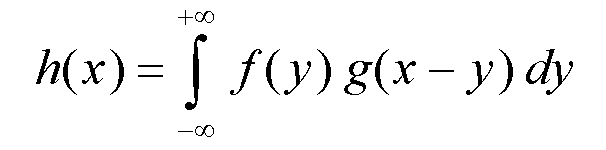
To deconvolute is obtaining
f knowing h and g.
This can be done by a
simple division in the Fourier space :
F(n) = H(n)/G(n).
Some limitations :
The Rietveld method is
intrinsically unable to consider diffuse scattering since it concentrates
on the Bragg scattering (hkl-based).
Nevertheless, some defects can be described reasonably as leading to a mean statistical effect inside the average cell (if small and uncorrelated atomic displacements).
Only those "periodical" defects can be seriously considered in a whole profile approach depending on a hkl-based description of the diffracted intensity.
If assimilation to a "periodical effect" is acceptable in the case of size line-broadening, this is much less evident for all the possible effects due to all kinds of dislocations or grain boundaries.
Indeed, dislocations and
grain boundaries are building locally some arrangements completely different
from the mean unit cell, but they certainly do have statistical effects
on the neighboring cells by displacing atoms trying ro resorb the faults.
Edge dislocation in a simple cubic crystal :
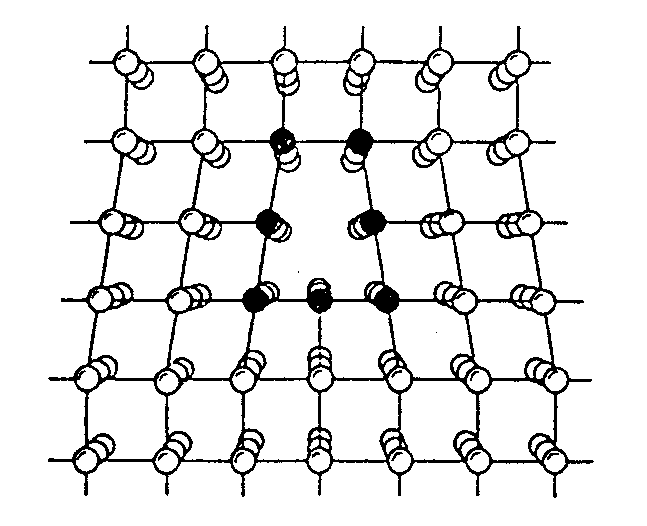
Atomic structure in the
core of grain boundary between two crystals, deduced from high-resolution
electron micrography :
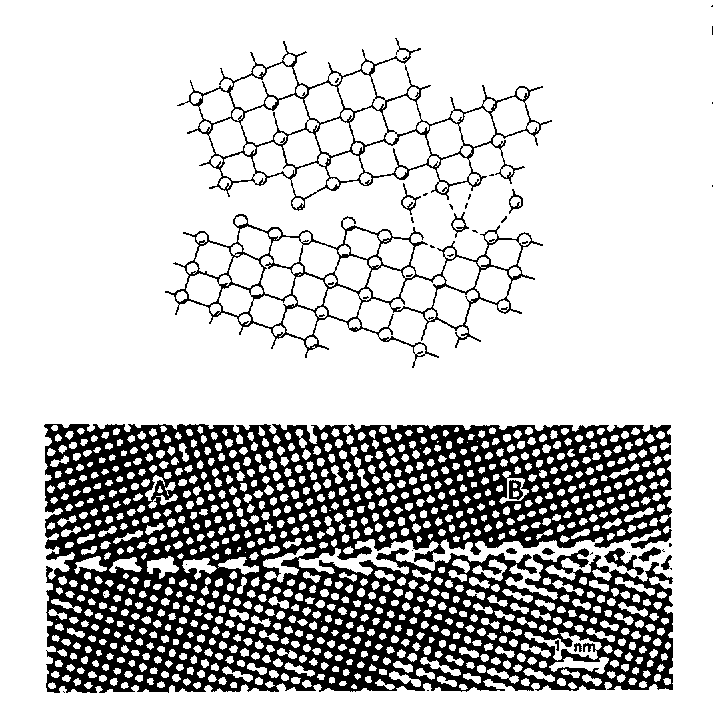
These examples are simple metallic compounds. What about similar effects in more complex compounds ?
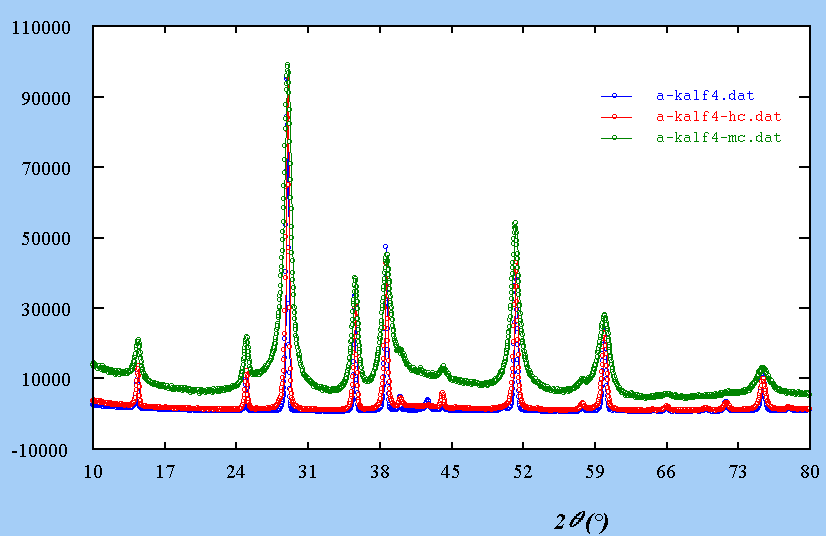
For instance, KAlF4, relatively simple, it has been shown that it may contain inclusions with another structure :

A single crystal laue
shows large diffusion effects :
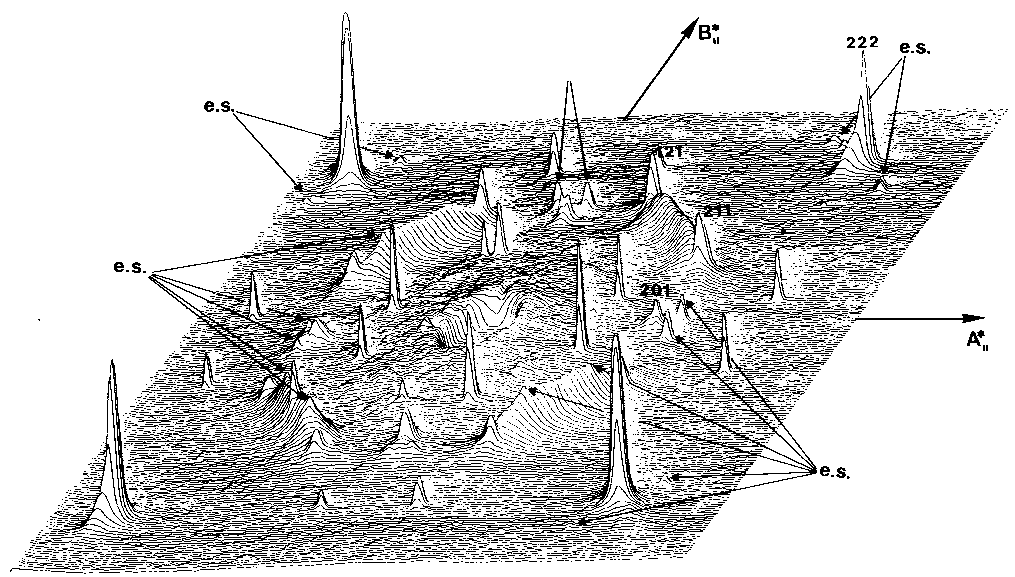
Extra spots are explained by those two structures imbricated :
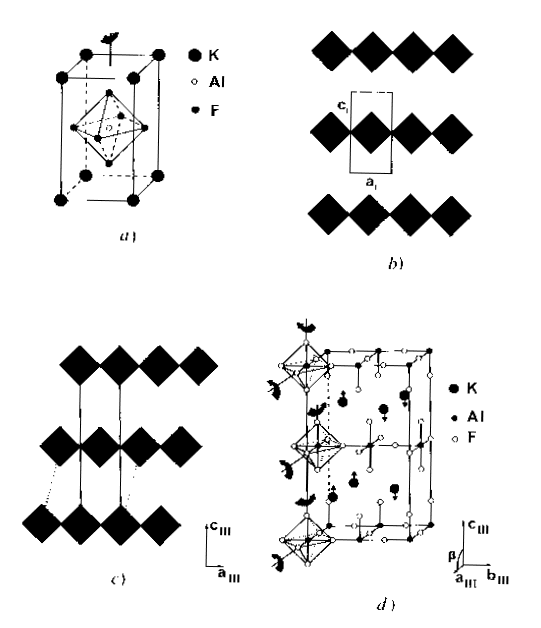
What is the effect on
a powder pattern ?
All is now at a one-dimensional
scale :